分子は一定の動きです。 彼らは固定位置を占有していないので、彼らの分離は絶えず変化しています。特定の瞬間に、それらの間の *平均距離 *についてのみ話すことができます。
平均距離は、物質の状態に依存します:
* ガス: 理想的なガスでは、分子は遠く離れており、ランダムに動きます。 平均距離は、容器の体積と分子数に関連しています。 理想的なガス法(PV =NRT)とAvogadroの数を使用して、平均分離を計算できます。
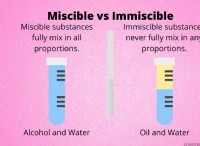
* 液体: 分子は液体で近くにありますが、それでも動き回っています。平均分離はガスよりも小さく、直接計算するのが難しいです。
* 固体: 分子は固体でしっかりと詰め込まれていますが、それでも振動します。 平均分離は、固体の結晶構造によって決定されます。
計算にアプローチする方法:
1。物質の状態を特定します。 これはあなたのアプローチを導きます。
2。理想的なガス法を考えてみましょう: ガスの場合、理想的なガス法は良い出発点を提供します。
* PV =NRT
* どこ:
* Pは圧力です
* Vはボリュームです
* nはモル数です
* rは理想的なガス定数です
* tは温度です
3。モル体積を計算します: 音量(v)をモル数(n)で除算します。これにより、1モルのガスが占めるボリュームが得られます。
4。平均分離を推定します: 分子がモル体積に等しい体積を持つ立方体に均等に分布すると仮定することにより、平均分離に近似できます。 キューブの副長さ(ボリュームのキューブルートを使用)を計算すると、分子間の平均距離の大まかな推定値が得られます。
重要なメモ:
* 平均分離は単なる近似です。 分子運動と相互作用は、距離が常に変化していることを意味します。
* 他の要因は平均距離に影響を与える可能性があります。 これらには以下が含まれます:
*分子の性質(サイズ、形状、極性)
* 温度
* プレッシャー
例:
標準温度と圧力(STP)で1モルの理想的なガスがあるとしましょう。 STPで:
* P =1 ATM
* T =273.15 K
* r =0.0821 L ATM/mol k
理想的なガス法を使用して、ボリュームを見つけることができます。
v =(nrt)/p =(1 mol * 0.0821 l atm/mol k * 273.15 k)/1atm≈22.4l
モル容積は22.4 Lです。分子が立方体に均等に分布すると仮定して、キューブの側面の長さは次のとおりです。
∛22.4L≈2.8l^(1/3)(これは分子間の平均距離です)。
これは非常に単純化された計算ですが、問題にアプローチする方法の感覚を与えます。より正確な推定のために、より複雑なモデルと要因を考慮する必要があります。