「傾斜面を滑り落ちるブロック」は、摩擦を扱う初年度のよくある宿題です。この問題は比較的単純な例の問題ですが、トリックを使用してさらに簡単にすることができます。これは大地を揺るがすトリックではありませんが、新しい物理学の学生が常に思いつくわけではありません。この古典的な問題のこの有効な解決策は、そのトリックを使用しています。
問題:
平らな面に重さ w の質量がある。ブロックがランプを一定の速度で滑り落ちるまで、サーフェスの一端を持ち上げます。ブロックと傾斜面の間の摩擦係数は?
解決策:
この図は、ブロックが動いているときに働く力を示しています。
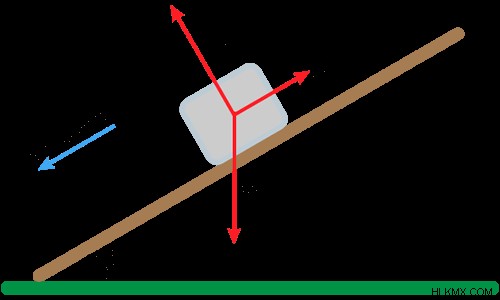
法線力 N は、ランプの表面に対して垂直です。摩擦力 Ff ランプの表面に平行に作用し、ブロックの動きに抵抗します。おもり w は垂直に下に引っ張ります。地面とランプの表面の間の角度は θ です。
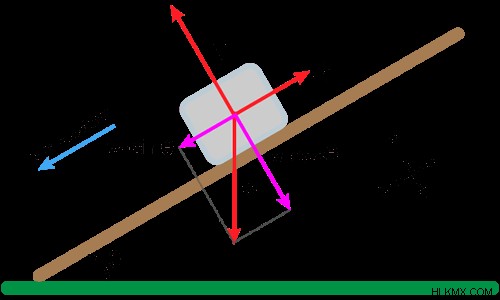
今トリックのために。ほとんどの生徒はすぐに座標系を地面と平行にします (上下、左右)。座標系を傾斜路の傾斜に揃えることを選択し、正の x 方向が傾斜路を下る場合、三角法を大幅に節約できます。ほら、私が言ったような大地の破壊ではありませんが、問題を単純化するのに非常に役立ちます.これで、力を x 成分と y 成分に分解できます。
x 方向の力の合計は次のとおりです。
ΣFx =w·sinθ – Ff
私たちは摩擦力 Ff を知っています =μN。ブロックが動いているので、使用する μ は動摩擦係数です:μk .
ΣFx =w・sinθ – μk N
システムは平衡 (一定速度) にあるため、すべての力の合計はゼロに等しくなります。
w·sinθ – μk N =0
また
w·sinθ =μk N
次にy方向です。この場合も、力の合計はゼロに等しくなります。
ΣFy =0
ΣFy =N – w·cosθ
0 =N – w・cosθ
また
N =w·cosθ
この解を x 方向から得た結果に当てはめます。
w·sinθ =μk (w·cosθ)
μk を解く
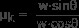

μk =tanθ
答え:
ブロックと傾斜面の表面との間の動摩擦係数は、ブロックが一定の速度で移動しているときに、地面とランプの表面との間に形成される角度の正接に等しくなります。
摩擦力、摩擦係数、および別の問題例の詳細については、次のリンクを参照してください:摩擦の例題 – 物理学の宿題ヘルプ.