* 粒子の質量(m): より大きな粒子は、同じ円運動を維持するために、より大きな中心力を必要とします。これは直接比例します。質量の2倍は、必要な中心力の倍増を意味します。
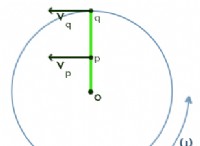
* 粒子の速度(v): 粒子が速く移動するほど、それを円で動かし続けるために必要な中心力が大きくなります。この関係は二乗されています。速度を2倍にするには、中心部の4倍が必要です。
* 円形経路の半径(r): 曲率の半径が小さくなるには、粒子を円に動かし続けるには、より大きな中心力が必要です。これは反比例して比例します。半径を半分にすることは、必要な中心力を2倍にすることを意味します。
中心力の式:
これらの要因間の関係は、次の方程式でキャプチャされます。
`` `
fc =(mv^2) / r
`` `
どこ:
* fc 中心部の力です
* m 粒子の質量です
* v 粒子の速度です
* r 円形経路の半径です
要約:
*質量、速度、または円形経路の半径を減らすと、均一な円運動を維持するために必要な中心力が増加します。