これが故障です:
1。往復スペース:
*繰り返しユニットセルで構成された結晶格子を想像してください。
* 実際のスペース この格子内の原子の位置について説明します。
* 相互空間 アトムの位置を記述する代わりに、波の波長と波の方向を説明する別の空間です それはクリスタル格子を通して伝播する可能性があります。
2。 Kポイント:
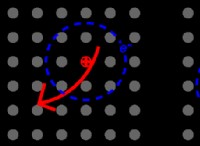
* kポイントは、相互空間のポイントです。 それらは、電子波の特定の波長と方向を表します。
*各kポイントは、特定の波動ベクトルに対応します 、 k で示されます 。
* kベクトルの大きさ 電子波の波長に反比例します。
* kベクトルの方向 電子波の伝播方向を示します。
3。 Kポイントが重要なのはなぜですか?
* 電子バンド構造: kポイントは、電子バンド構造を計算するために重要です 材料の。バンド構造は、材料内の電子の許容エネルギーレベルを説明し、最終的には電気、光学、磁気特性を決定します。
* Blochの定理: 周期的な結晶では、電子は bloch波のように動作します 、平面波によって変調される周期的な関数です。 kポイントは、波のベクトルを記述するために使用されます これらのブロックの波の。
* 密度機能理論(DFT): 材料の電子構造を計算するために使用される一般的な方法には、結晶内の電子のシュレディンガー方程式を解くことが含まれます。 DFT計算には、 kポイントのサンプリングが含まれることがよくあります 電子バンド構造の適切な表現を得るための相互の空間で。
4。実用的な考慮事項:
* kポイントの数: 計算で使用されるKポイントの数は、結果の精度に影響します。 Kポイントが多いほど精度が高くなりますが、より多くの計算リソースも必要です。
* k-pointメッシュ: 相互空間を効果的にサンプリングするために、kポイントはメッシュに配置されることがよくあります ポイントの。メッシュの密度は、ユニットセルのサイズと複雑さ、および望ましい精度に依存します。
* 高い対称点: 相互空間のいくつかのkポイントは、結晶格子の高い対称点に対応しています。これらのポイントは、電子構造に関する貴重な情報を提供するため、多くの場合、特別な計算のために選択されます。
要約:
Kポイントは、固体物理学の基本的な概念です。それらは、相互空間における電子波の特定の波長と方向を表します。彼らは、材料の動作に影響を与える重要な特性である電子バンド構造を決定する上で重要な役割を果たします。 Kポイントを理解することは、固体の電気的、光学的、磁気特性を研究および予測するために不可欠です。