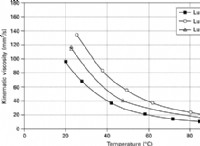
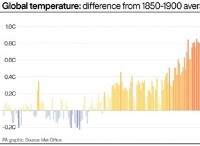
結果の波
等しい周波数と振幅の2本の正弦波を重ねると、結果として生じる波も正弦波です。ただし、結果の波の振幅と位相は、元の波の相差に依存します。
* フェーズ: 2つの波が位相にある場合(ピークとトラフが整列)、結果の波には個々の波の2倍の振幅があります。
* フェーズ外: 2つの波が位相が外れている場合(1つの波のピークが他方のトラフと整列します)、結果の波はゼロの振幅を持ちます。これは、波がお互いを完全にキャンセルすることを意味します。
* 中間相の差: 位相内と位相が外れている間の位相差の場合、結果の波は、元の振幅のゼロから2倍の間のどこかに振幅を持ちます。正確な振幅は、特定の位相差に依存します。
粒子に何が起こるか
得られた波にさらされた粒子は、元の波の周波数に等しい周波数で振動します。ただし、粒子の振動の振幅は、元の波の位相差に依存します。
* フェーズ: 粒子は、個々の波の2倍の振幅で振動します。
* フェーズ外: 粒子はまったく振動しません。
* 中間相の差: 粒子は、位相差に応じて、元の振幅のゼロから2倍の間の振幅で振動します。
重要な概念
* 重ね合わせ: 波が出会うと、振幅が一緒になります。
* 位相差: 2つの波の開始位置(位相)の違い。
* 振幅: その平衡位置からの波の最大変位。
効果を視覚化する
この現象を、一方の端で結び付けた2つのロープを想像することで視覚化できます。同じ周波数と振幅で両方のロープを振ると、波はロープを下って移動して結合します。結果として生じる波は、互いにロープがどのように揺れるかに依存します。
特定の側面について詳しく説明するか、より詳細な数学的説明を提供してほしいかどうかを教えてください!