1。概念を理解する
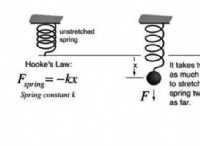
* 重力(mg): これは、地球の表面近くの重力によるおおよその力です。一定の重力加速度(g)を想定しています。
* 実際の重力: これは、地球の中心からの距離とともに重力が減少する逆平方法を考慮に入れます。
2。方程式を設定します
近似力と実際の重力の違いが4%である高さ(h)を見つけたいと思います。 させて:
* * g *地球の表面の重力による加速(〜9.8 m/s²)
* * g *重力定数(〜6.674 x10⁻¹¹nm²/kg²)
* * m *地球の質量(〜5.972 x10²⁴kg)
* * r *地球の半径になる(〜6.371x10⁶m)
* * m *オブジェクトの質量になります
近似力は次のとおりです。 *f_approx *=*mg *
実際の力は: *f_actual *=*gmm /(r + h)² *
*(f_actual -f_approx) / f_approx * =0.04
3。高さ(h)を解きます
* f_actual *および * f_approx *の式を方程式に置き換えます。
[(gmm /(r + h)²)-mg] / mg =0.04
簡素化:
[gm /(r + h)² -g] / g =0.04
[gm /(r + h)²] / g =1.04
gm /(r + h)²=1.04g
(r + h)²=gm /(1.04g)
r + h =√(gm /(1.04g))
h =√(gm /(1.04g))-r
4。高さを計算します
*g *、 *m *、 *g *、および *r *の値をプラグインします。地球の半径をキロメートルに変換することを忘れないでください。
h =√((6.674 x10⁻¹¹nm²/kg²) *(5.972 x10²⁴kg)/(1.04 * 9.8 m/s²)-6.371 x10⁶m
H≈3.27x10⁶m≈ 3270 km
したがって、地球の表面から約3270キロメートルの高さで、おおよその重力と実際の重力力の間には約4%の差があります。