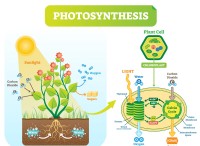
その理由は次のとおりです。
* ニュートンの普遍的重力の法則: この法律は、2つのオブジェクト間の重力は、質量の積に比例し、中心間の距離の平方に反比例すると述べています。
* 力と加速: ニュートンの第二の運動法則は、オブジェクトに作用する力はその質量倍その加速(f =ma)に等しいと述べています。
* 法律の組み合わせ: 体が自由に落ちると、それに作用する力は重力です。 重力(FG)は、落下体(m):Fg =gm1m2/r²の質量に比例します。ここで、gは重力定数、m1は地球の質量、m2は低下体の質量、rは中心間の距離です。
* 質量のキャンセル: 重力の力を落下体の質量に等しく設定すると、その加速時間(FG =MA)があります。GM1M2/R²=MAが取得されます。 落下体(M2)の質量は両側でキャンセルされ、加速(A)=GM1/R²が残ります。
したがって、重力による加速は、地球の質量(M1)と地球の中心と落下体(R)の間の距離にのみ依存します。
注: これは真空でのみ当てはまります。空気抵抗は落下物の加速に影響を与える可能性があり、その影響は、表面積と質量の比率が大きいため、より軽いオブジェクトにとってより重要です。