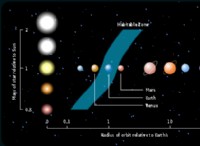
* ケプラーの第二法則: この法律では、惑星は等しい領域で等しい領域を一掃すると述べています。これは、惑星が太陽に近づくと、より速く動き、遠く離れていると動きが遅くなることを意味します。
* エネルギーの保存: 惑星の総エネルギー(運動 +電位)は、軌道全体で一定のままです。惑星が太陽に近づくと、そのポテンシャルエネルギーが減少し(重力引力のため)、これは運動エネルギーの増加によって補償され、スピードアップされます。反対は、それが遠く離れて移動するときに起こります。
速度の計算:
軌道の特定のポイントでの惑星の速度は、 vis-viva方程式を使用して計算できます。
v²=gm(2/r -1/a)
どこ:
* vは軌道速度です
* gは重力定数です
* mは太陽の質量です
* rは、その時点で惑星から太陽までの距離です
* aは軌道の半長軸です
重要なポイント:
*速度は、近期で最大です (太陽に最も近い点)。
*速度は aphelion で最小です (太陽から最も遠い点)。
*軌道全体の平均速度は計算できますが、特定のポイントでの速度を表しません。
他に質問がある場合はお知らせください!