1。変化率の記述:
* 線形関係: スロープは、別の数量のユニットごとに変化する量を測定します。線形関係の変化率を教えてくれます。 たとえば、距離と時間を表すグラフ上の線の勾配は、オブジェクトがどれだけ速く移動しているかを示します。
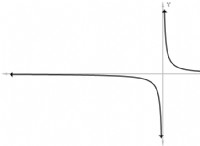
* 非線形関係: 勾配は曲線に直接適用できませんが、その導関数(瞬時の変化速度)は、特定のポイントで機能がどのように変化するかを理解するために計算で重要です。
2。将来の値の予測:
* 線形外挿: 勾配を知ることで、現在の値と変化率に基づいて変数の将来の値を予測することができます。これは、予測、トレンド分析、および計画に使用されます。
3。関係を理解する:
* 直接比例: 正の勾配は、2つの変数間の直接的な関係を示します。つまり、それらが一緒に増加または減少することを意味します。
* 逆比例率: 負の勾配は逆の関係を示します。つまり、1つの変数が他の変数が減少するにつれて増加します。
4。実用的なアプリケーション:
* エンジニアリング: 勾配は、安定性と機能性を確保するために、道路、橋、その他の構造の設計に使用されます。
* 構造: 斜面は、屋根、ランプ、その他の要素の角度を決定するために重要です。
* 財務: Slopeは、株価やその他の財務データの分析に使用され、傾向を特定し、投資決定を下します。
* 天気: 勾配は、気象パターンを予測し、空気塊の動きを理解するために使用されます。
* 薬: 勾配は、患者のバイタルサインの変化率を分析し、病状を診断するのに役立ちます。
5。数学的基礎:
* 計算: 勾配は、計算の基本的な概念であり、変化、最適化、および他の多くの数学の領域を理解するために不可欠です。
* 線形代数: Slopeは、線形代数の重要な概念であり、線形方程式とそのソリューションのシステムを扱っています。
要するに、Slopeは、変数間の関係を理解し、将来の値を予測し、さまざまな分野の問題を解決するのに役立つ強力なツールです。これは、幅広いアプリケーションを備えた基本的な概念です。