数学では、関数の漸近線は、関数が無限に近づくが決して到達しない線です。より正確な数学的用語では、曲線の漸近線は、曲線の x 座標と y 座標の一方または両方が無限大に向かう傾向があるため、線と曲線の間の距離が 0 に近づくような線として定義できます。言い換えると、漸近線は、関数が永遠に近づくグラフ上の線ですが、実際には到達することはありません.
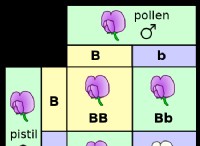
漸近線には主に 3 種類あります。垂直、水平、斜め。それぞれ、座標平面に対する向きに基づいて定義されます。垂直漸近線は、最も一般的で簡単に決定できる漸近線です。垂直漸近線は、勾配が定義されていない直線と同等です。つまり、有理関数の垂直漸近線は、その有理関数の分母を 0 に設定する x 値に配置されます。有理関数は、2 つの多項式の商として表される関数です。たとえば、有理関数ƒ(xのグラフ ) =1/x ² 次のようになります:
x を 0 に設定すると、有理関数 ƒ(x の分母が設定されます。 ) =1/x ² から 0 へ。したがって、この関数は x=0 の線に位置する垂直漸近線を持ちます。垂直漸近線は、1 つのグラフが複数の垂直漸近線を持つことができるという点で独特です。逆に、グラフには最大で 1 つの水平漸近線または 1 つの斜め漸近線のみを含めることができます。
漸近線の概念
最初は、漸近線の概念は私たちの日常の経験に反しているように見えます。紙の線やコンピューター画面のピクセルなど、グラフ上の曲線の物理的な表現には、有限の幅があります。これらの線を十分に延長することで、曲線は最終的に、または少なくとも私たちの視覚でわかる限り、漸近線に一致するように見えます。グラフは、理想化された数学的実体の物理的表現であることを覚えておく必要があります。理想化された幾何学的な線の幅は 0 であるため、数学的な線は、実際に一致することなく何かにどんどん近づいていく可能性があります。
「ある量が近づくが決して到達しない値」という概念は、ある意味では、変化、運動、連続性に関する古代ギリシャのパラドックスにその起源を見出していると考えることができます。これは、エレアのゼノによって与えられた有名な例です。偉大なアスリートのアキレスが 100 メートルのダッシュを走っています。 100メートル走るためには、まず半分の距離を走らなければならないので、50メートル走ります。残りの 50 メートルを走るには、まずその距離の半分、つまり 25 メートルを走らなければなりません。残りの 25 メートルをカバーするには、まずその距離の半分、つまり 12.5 メートルをカバーする必要があります。残りの 12.5 メートルを横断するには、まずその距離の半分、つまり 6.25 メートルを横断する必要があります。
この推論を外挿する 無限 アキレスは絶対しないという直観に反する結論に導きます フィニッシュラインを越える。 常にあります 彼が最初に渡らなければならない有限の距離であるため、実際にフィニッシュラインに到達することはありません.哲学者と数学者は、何世紀にもわたってゼノンのパラドックスについて頭を悩ませてきました。ゼノには知られていないが、彼の運動のパラドックスは、現代の数学的漸近線の概念を捉えることに非常に近づいている.
垂直漸近線の定義
漸近線の最初の正式な定義は、微積分における極限の概念と並行して生じました。関数の極限とは、パラメーターの 1 つが無限大になる傾向があるときに関数が近づく値です。したがって、関数には、その値での方程式の限界が無限大になるような値として漸近線があります。
垂直漸近線は最も一般的で、決定が容易であるため、ここでは垂直漸近線のみを考慮します。関数に垂直漸近線があるかどうかを判断するための一般的な条件は次のとおりです。関数 ƒ(x) が垂直漸近線を持つのは、x が a .つまり、関数の限界が a は無限に等しい.
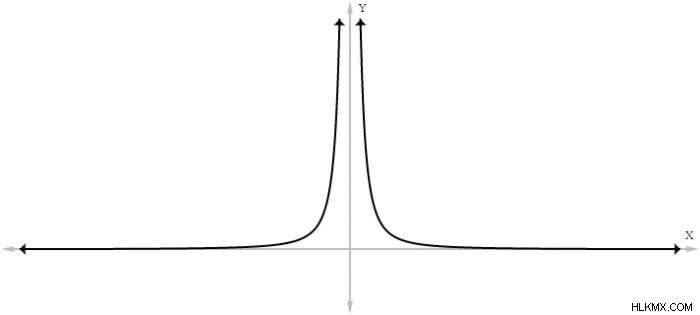
最後の段落は長すぎたので、簡単な例を見てこのアイデアを具体化しましょう。以下は関数ƒ(x) =1/xのグラフです:
この関数は逆曲線の形を取ります。 x の値が両側から 0 に近づくときの関数の動作に注意してください。 x の値が 0 に近づくにつれて、関数は正と負の両方の方向に際限なく急速に成長し始めます。どんどん 0 に近づいていく x 値を関数に代入し始めるとどうなるか見てみましょう:
ƒ(1) =1/1 =1
ƒ(0.5) =1/0.5 =2
ƒ(0.25) =1/0.25 =4
ƒ(0.1) =1/0.1 =10
ƒ(0.01) =1/0.01 =100
ƒ(0.001) =1/0.001 =1000
ƒ(0.000001) =1/0.000001 =1,000,000
ƒ(0.00000001) =1/0.00000001 =1億
x が 0 に近づくと、関数の出力が無限大に向かって正の方向に任意に大きくなることに注意してください。最も重要なことは、関数が f(0) に対して定義されていないため、関数が x=0 で線を超えることはありません (1/0 は通常の算術では定義されていません)。同様に、左から 0 に近づくと、値は次のようになります
ƒ(-0.5) =1/-0.5 =-2
ƒ(-0.25) =1/-0.25 =-4
ƒ(-0.1) =1/-0.1 =-10
ƒ(-0.01) =1/-0.01 =-100
ƒ(-0.001) =1/-0.001 =-1000
ƒ(-0.000001) =1/-0.000001 =-1,000,000
ƒ(-0.00000001) =1/-0.00000001 =-1億
x が左から 0 に近づくにつれて、関数の出力は負の無限大に向かって負の方向に任意に大きくなります。どちらかの側から漸近線に近づくと、関数はいずれかの方向に任意に大きくなるため、これは両側漸近線です。一部の関数は、片側からのみ漸近線にアプローチします。
垂直漸近線を見つける方法
有理関数の垂直漸近線を見つけるのは比較的簡単です。有理関数の分母を 0 に設定する x の値を見つけるだけです。簡単な例を次に示します。
関数ƒ(x) =(x+4)/3(x-3)の垂直漸近線は?
これは簡単です。分母 tern 3(x-3) が 0 になるような x の値を見つけるだけです。しばらく観察すると、答えは x= であることがわかります。 3;関数 ƒ(x) =(x+4)/3(x-3) は x=3 で垂直漸近線を持ちます。
直接計算する代わりに、有理関数をグラフ化することが、その関数に漸近線があるかどうかを判断するのに役立つ場合があります。関数ƒ(x) =(x+4)/(x-3)のグラフは次のようになります。 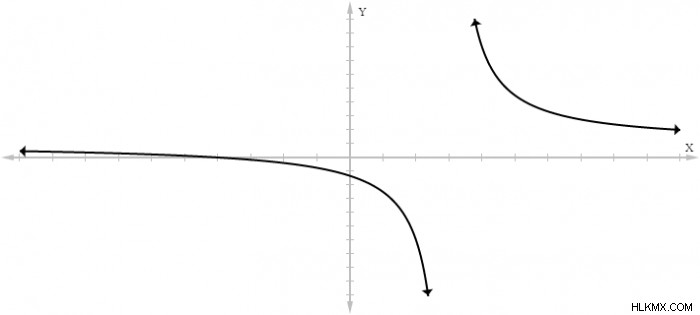
x が左右から 3 に近づくと、関数はそれぞれ負の無限大と正の無限大に向かって際限なく成長することに注意してください。グラフを見るだけでは、関数に垂直漸近線があることを証明することはできませんが、グラフを探すときの出発点としては便利です。
ソリューションに関するその他の問題
垂直漸近線を見つけることに慣れるために、さらにいくつかの問題を見てみましょう。
(1)
関数ƒ(x) =(x+2)/(x²+2x−8)の垂直漸近線は?
解決策:
ここでも、分母項を 0 に設定する x 値を見つける必要があります。この場合、分母項は (x²+2x−8) です。この項を 0 にする x の値は、因数分解によって求めることができます。因数分解 (x²+2x−8) により、次の結果が得られます:
(x²+2x−8) =(x+4)(x-2)
この関数には、実際には、分母の項を 0 に設定する 2 つの x 値、x=-4 および x=2 があります。 したがって、関数 ƒ(x) =(x+2)/(x²+2x−8) には、-4 と 2 に 2 つの漸近線があります。この方程式をグラフにすると、次のようになります。 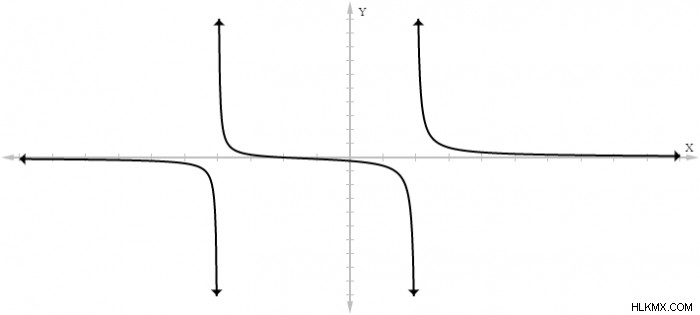
方程式をグラフ化すると、関数には x 値 -4 と 2 に位置する 2 つの垂直漸近線があることがわかります。
(2)
関数ƒ(x) =(x³−8)/(x²+9)の漸近線は?
解決策:
これを理解するには、分母を 0 に設定する必要があります。
x²+9 =0
x² =-9
おっと!この方程式には解がありません。任意の数の二乗は常に 0 よりも大きいため、x² が -9 に等しいような x の値はありません。したがって、分母を 0 に設定できる x 値はないため、関数ƒ(x) =(x+2)/(x²+2x−8) には垂直方向の漸近線がありません!
(3)
関数ƒ(x) =x/(x²+5x+6)の漸近線は?
解決策:
繰り返しになりますが、分母の項を因数分解して項を 0 に設定する x の値を見つけることで、この問題を解決できます。下の項 x²+5x+6 を因数分解すると、次のようになります。
x²+5x+6 =(x+2)(x+3)
この多項式には、x=-2 と x=-3 の 2 つの値があり、0 に設定されます。 したがって、関数ƒ(x) =x/(x²+5x+6)には、x=-2とx=-3に2つの垂直漸近線があります。 この関数をグラフにすると、次のようになります。 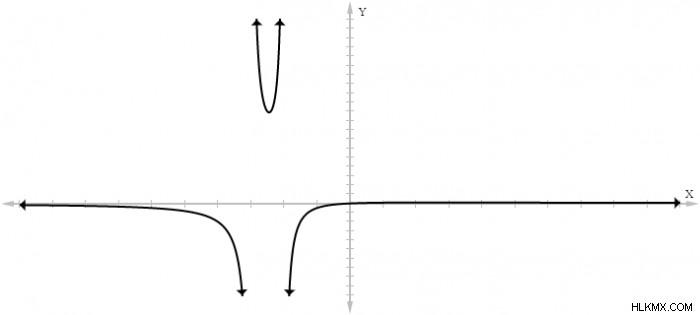
このグラフが左から -3 に、右から -2 に近づくにつれて、関数は負の無限大に近づきます。右から -3、左から -2 に近づくにつれて、関数は無限大に向かって際限なく成長します。これら 2 つの漸近線の配置により、グラフは 3 つの異なる部分に分割されます。
要約すると、垂直漸近線は、関数のパラメーターの 1 つが無限大に近づくにつれて、関数が近づく垂直線です。関数は永遠に漸近線に近づきますが、実際には触れません。関数が a に近づくときの関数の極限が正または負の無限大になるような x=a がある場合にのみ、関数は垂直漸近線を持ちます。分母項を 0 に設定する x 値を見つけることで、有理関数の垂直漸近線を決定できます。