一定の加速度の下での直線運動は、一般的な物理学の宿題です。それらに関連する問題を解決するために使用できるこれらの条件を説明する運動方程式。これらの方程式は次のとおりです:
(1) x =x0 + v0 t + ½at
(2) v =v0 +で
(3) v =v0 + 2a(x – x<サブ>0 )
どこ
xは移動距離
x0 最初の出発点です
vは速度です
v0 は初速度
a は加速度
t は時間です
この問題例は、これらの方程式を使用して、絶えず加速している物体の位置、速度、および時間を計算する方法を示しています。
例:
ブロックは摩擦のない表面を 2 m/s の一定の加速度で滑ります。時間 t =0 秒で、ブロックは x =5m にあり、速度 3 m/s で移動します。
a) t =2 秒のブロックはどこにありますか?
b) 2 秒でのブロックの速度は?
c) 速度が 10 m/s のとき、ブロックはどこにありますか?
d) ここまで来るのにどれくらいかかりましたか?
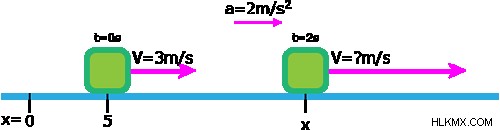
解決策:
これはセットアップの図です。
私たちが知っている変数は次のとおりです。
x0 =5m
v0 =3 メートル/秒
a =2 メートル/秒
パート a) t =2 秒でブロックはどこにある?
式 1 は、この部分に役立つ式です。
x =x0 + v0 t + ½at
t に t =2 秒を代入し、x0 の適切な値を代入します。 そして v0 .
x =5m + (3m/s)(2s) + ½(2m/s)(2s)
x =5m + 6m + 4m
x =15 m
ブロックは t =2 秒で 15 メートルのマークにあります。
パート b) t =2 秒でのブロックの速度は?
今回は、方程式 2 が有用な方程式です。
v =v0 +で
v =(3 メートル/秒) + (2 メートル/秒)(2 秒)
v =3 メートル/秒 + 4 メートル/秒
v =7 メートル/秒
ブロックは t =2 秒で 7 m/s で移動しています。
パート c) 速度が 10 m/s のとき、ブロックはどこにありますか?
現時点では式 3 が最も有用です。
v =v0 + 2a(x – x<サブ>0 )
(10m/秒) =(3m/秒) + 2(2m/秒)(x – 5m)
100m/s =9m/s + 4m/s(x – 5m)
91m/s =4m/s(x – 5m)
22.75m =x – 5m
27.75 m =x
ブロックは 27.75 m マークにあります。
パート d) この点に到達するのにどのくらいかかりましたか?
これを行うには 2 つの方法があります。方程式 1 を使用して、問題のパート c で計算した値を使用して t を解くか、方程式 2 を使用して t を解くことができます。式 2 の方が簡単です。
v =v0 +で
10m/s =3m/s + (2m/s)t
7 メートル/秒 =(2 メートル/秒)t
⁄2 s =t
⁄2かかります 秒または 3.5 秒で 27.75 m マークに到達します。
このタイプの問題の厄介な部分の 1 つは、質問が何を求めているのかに注意を払わなければならないことです。この場合、ブロックが移動した距離ではなく、どこにあるかが尋ねられました。基準点は原点から 5 メートルです。ブロックが移動した距離を知る必要がある場合は、5 メートルを引く必要があります。
さらにヘルプが必要な場合は、これらの運動方程式の例の問題を試してください。
運動方程式 – 傍受の例
運動方程式 - 垂直運動
運動方程式 – 車両の破壊
運動方程式 – 発射物の運動