Atwood Machine – 慣性の例題

アトウッド マシンは、一定の加速度を受ける 2 つの結合されたシステムの運動の法則を示す一般的な教室での実験です。アトウッド マシンは 2 つの質量 m_A で構成されています そして m_B 、質量のないプーリー上の非伸縮性の質量のない糸によって結合されています。 2 つの質量が等しい場合、システムは平衡状態にあり、運動は発生しません。 2 つの質量は静止したままになります。 2 つの重量が等しくない場合、システムは、重い方の質量が引き下げられ、軽い方の質量が引き上げられる場所に移動します。この問題例は、システムの加速度と弦の張力を導き出す方法を示しています。

問題:
a) m_A の場合、アトウッド マシンの加速度を求めます。 =3 kg と m_B =5キロ。
b) 2 つの質量をつなぐ弦の張力を見つけます。

これはセットアップの図です。

m_A の値は無視します そして m_B この時点で、答えの導出を示します。ブロック B はブロック A よりも重いため、全体的な動きの方向は、滑車のブロック B 側で下向きになり、ブロック A 側で上向きになります。加速度が常に正になるように座標系を選択してください。

このシステムは、質量のないストリングによって結合されています。より重いブロック B は、ある時間 t で距離 Δd だけ弦を引き下げます。同時に、ブロック A は Δd 上に移動します。つまり、各ブロックの速度は同じです。

v_A =⁄_t =v_B

速度方向は、各システムに選択された座標系によって調整できます。速度は常に同じなので、加速度も同じです。

a =a_A =a_B

弦は質量がなく、伸びないため、張力はシステム全体で均一です。ブロック A を引き上げる張力は、ブロック B を引き上げる張力と同じです。

これは、加速度と張力が両方のブロックで同じであることを意味します。次に、各ブロックに作用する力を見つけます。

ブロック A の重み m_A g は引き下げられ、張力 T は引き上げられます。

ΣF =T – m_A g

これらの力は動いているので、これらの力はm_Aに等しい a.

ΣF =m_A a =T – m_A g

ブロック B では、力はほぼ同じです。違いは、全体的な加速度がブロック A の反対方向にあることです。

ΣF =m_B g – T =m_B

これで、2 つの方程式と 2 つの未知数、T と a ができました。これらの 2 つの方程式を一緒に追加すると、T は脱落し、加速度だけが残ります。

m_A a =T – m_A g
m_B a =-T + m_B g
m_A a + m_B a =m_B g – m_A g

両側の加速度変数と重力変数を計算してください。

(m_A + m_B )a =(m_B – m_A )g

両辺を (m_A + m_B ) を解く。

加速度があるので、これを使用して、2 つの力の方程式のいずれかを使用して張力を見つけることができます。ブロック A を使いましょう。

m_A a =T – m_A g

これを T について解いて、以下を取得します。

T =m_A a + m_A g

加速度 (a) の式を式に代入します。

式を次のように書き換えます。

m_A を因数分解する g

1 を変更して、括弧内に共通の分母を持たせます。

2 つの分数を足して、

単純化して取得

なる

これらの加速度と張力の式を使用して、最初の問題に対する答えを見つけてください。

パート a) m_A のときの加速度を求める =3 kg と m_B =5kg。

前に、加速度の式は

m_A の値を入力してください そして m_B .


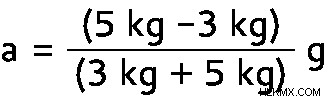
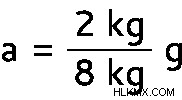
a =2/8 グラム
a =0.25 (9.8 メートル/秒)
a =2.54 メートル/秒

ブロックは 2.54 m/s で加速しています。

パート b) 弦の張力を見つけます。

T =36.75 kg·m/s

kg・m/sは力のニュートン単位と同じです。

T =36.75 N

弦の張力は 36.75 ニュートンです。

ヒント:

このタイプの問題の鍵は、加速度の方向が常に正の方向になるように座標系を選択することです。加速度がすべて一緒に作用している限り、符号エラーは問題になりません。アトウッド マシンの場合、加速は常に大きな質量に向かって実行されます。