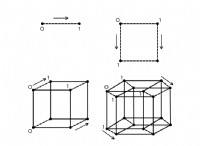
積分を見つけるには、面積の合計が必要です。同様に、定積分は、始点と終点の間の面積を計算するのに役立ちます。これが限界と言えます。曲線 f(x) の x 軸に関する面積を求める極限点として [a, b] を取ると、定積分の式は ∫baf(x)dx∫abf(x)dx となります。定積分と、定積分を使用して極限を見つける方法について詳しく説明しましょう。
定積分の定義
第 9 の標準では、始点と終点の間の曲線の下の面積を、長方形の面積を分割して合計することで計算していました。つまり、分割した領域を無数の長方形に追加していました。面積の精度は、長方形の数に正比例しました。したがって、定積分を曲線の 2 つの極限の間の領域として定義できます。
定積分を求める
定積分を求めるには、次の定積分の 2 つの式のいずれかを使用します。
- 微積分の基本定理
∫abf (x)dx=F(b)−F(a)、ここで F'(x) =f(x)
- 定積分を使用した極限とも呼ばれる極限和としての定積分
abf (x)dx=n∞ r=1nf(a+rh)/h
ここで h=b-an
微積分公式の基本定理による定積分
微分積分の基本定理は、定積分を計算する最も簡単な方法です。それを使用して、最初に f(x) の反導関数を見つけ (そしてそれを F(x) で表します)、最初に上限を代入し、次に個別に下限を下げることによって、次数の結果を減算する必要があります。 /P>
微分積分の基本定理(FTC)を使用して、A 定積分 ∫abf (x)dx を計算します。この式は ∫abf (x)dx=F(b)−F(a) で、F'(x) =f(x)
例:この定積分公式を使用して ∫01 x2dx を解きます。
微分積分の基本定理を使用して定積分を解く規則に従って、
まず、積分公式を使用して ∫x2dx を解きましょう。
解いた後、∫x2dx =x3/3 + C が得られます。
ここで、上限と下限を置き換えて違いを見つけます。
∫01 x2dx=(13/3 + C) – (03/3 + C) =1/3.
C は定数積分 C であり、定積分を解くときに常にキャンセルされるため、無視できます。
極限和式としての定積分
定積分を使用して曲線の面積を求めますが、これには 2 つの制限があります。面積は、2 つの境界で囲まれた四角形の数を計算することによって測定されます。この概念を使用して、定積分 ∫abf(x)dx を評価するために、[a, b] を無限の部分区間に分割することにより、曲線領域を多くの長方形に分割します。したがって、極限和式としての定積分は次のとおりです。
∫abf (x)dx=limn→∞ ∑r=1n1hf(a+rh)
ここで、h=b−anh=b−an は各サブインターバルの長さです。
例:上記の式を使用して 01x2dx を評価します。
積分を abf (x)dx、[a, b] =[0, 1] および f(x) =x2 と比較します。次に、h =(1 – 0)/n =1/n です。上記の式を適用すると、
01x2dx=n∞ r=1nf(0+r/n) /n
=n∞ r=1n(r/n)2 /n
=n∞1/n3r=1nr2
=n∞1/n3⋅n(n+1)(2n+1)/6 (加算式を使用)
=n∞(1/n3)n3(1+1/n)(2+1/n)/6
=(1+0)(2+0)/6
=1/3
定積分の規則
定積分を計算するには、プロパティの積分を決定し、関数の積分和、定数を掛けた関数、および偶数関数と奇数関数を見つけるのに役立つため、その規則も知っておく必要があります。次のルールは、定積分を計算するのに役立ちます:
- abf (x).dx=abf (t).dt
- ab-f (x).dx=−abf (x).dx
- abc f (x).dx=cabf (x).dx
- abf (x)±g(x).dx=abf (x).dx±abg(x).dx
- abf (x).dx=∫acf (x).dx+∫cbf (x).dx
- abf (x).dx=abf (a+b−x).dx
- 0a f(x).dx=0a f (a−x).dx (これは上記の式から派生した式です。)
- 02a f (x).dx=2 0af(x).dx if f(2a – x) =f(x)
- 02a f (x).dx=0 if f(2a – x) =-f(x).
- -aaf(x).dx=2 ∫0a f(x).dx、f(x) が偶関数の場合 (つまり、f(-x) =f(x))。
- -aa f(x).dx=0、f(x) が奇関数の場合 (つまり、f(-x) =-f(x))
結論
したがって、定積分を使用することにより、制限の下の曲線領域を計算できます。定積分を使用した極限の例から、定積分を評価して極限を計算する方法も理解できます。