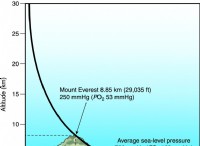
$$ \ text {acceleration(a)} =\ frac {\ text {and in velocity(∆V)}} {\ text {change in time(∆t)}} $$
さて、2つのケースを考えてみましょう。
ケース1:均一な加速:
オブジェクトの加速度が均一で、初期速度と同じ方向にある場合、次の方程式を使用して、最終速度(VF)を使用して決定できます。
$$ \ text {vf} =\ text {vi} + \ text {at} $$
-VIは初期速度を表します。
- aは一定の加速を表します。
ケース2:可変加速:
加速度が初期速度とは異なる方向である場合、時間間隔(∆T)にわたる平均加速度(AAVG)を使用して、速度(∆V)の変化を計算できます。
$$ \ text {∆V} =\ text {aavg} \ times \ text {∆t} $$
$$ \ text {vf} =\ text {vi} + \ text {∆V} $$
どちらの場合も、加速度は速度の変化に直接関係しています。より高い加速度は、速度の変化速度の速い速度に対応しますが、加速度が低いと速度の変化が遅くなります。
したがって、速度と加速度の関係は、次のように要約できます。
- 直接的な関係: 加速は、オブジェクトの速度の変化に直接比例します。
- 陽性加速: 加速度が陽性の場合(運動の方向)、速度が増加します。
- 負の加速: 加速度が負の場合(運動方向とは反対)、速度は低下します。