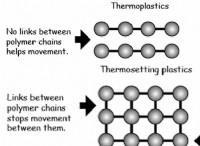
その理由は次のとおりです。
* 角運動量: 角運動量は、オブジェクトの回転傾向の尺度です。オブジェクトの質量、速度、および回転軸からの距離に依存します。
* 角運動量の保存: 外部トルク(ねじれ力)がない場合、システムの総角運動量は一定のままです。
* 軌道運動: 軌道運動では、軌道体と中心体の間の重力は中心力として作用します。この力は、2つの体をつなぐ線に沿って作用し、したがってトルクを生成しません。
したがって、軌道運動のシステムの角運動量は一定のままです。 この原則は、惑星、衛星、その他の天体の行動を理解する上で不可欠です。
ここに、軌道運動における角運動量の保存のいくつかの意味があります:
* ケプラーの第二法則: 法律は、惑星が同等の領域で等しい領域を一掃すると述べています。これは、角運動量の保存の直接的な結果です。
* 軌道形状の変化: 外力がシステムに作用し、トルクを引き起こすと、角運動量が変化する可能性があります。これにより、軌道をより楕円形にするなど、軌道の形状が変化する可能性があります。
* Tidal Locking: 月の回転は、地球の周りの軌道に激しくロックされています。これは、軌道と同じ速度で回転することを意味し、1つの顔を常に地球に面しています。このロックは、地球の回転から月の軌道運動への角運動量の移動の結果です。