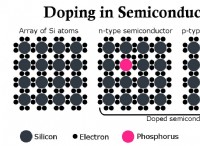
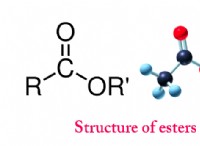
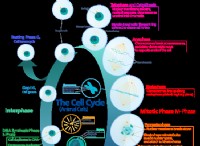
1。自由なボディ図を描きます
ランプにボックスの図を描きます。 箱に作用する力は次のとおりです。
* 重量(mg): これは垂直方向に下方に作用します。
* 通常の力(n): これはランプに対して垂直に作用し、ランプに箱を押します。
* 適用力(f): これは水平に作用します。
2。力を解決
* 重量: 重量力をランプに平行で垂直なコンポーネントに分割します。
* * mg * sin(25°)(ランプと平行、下方に行動する)
* * mg * cos(25°)(ランプに垂直)
* 通常の力: 通常の力は、重量の垂直成分のバランスをとる: * n * =* mg * cos(25°)
3。ニュートンの第二法則を適用します
ボックスは一定の速度で移動するため、それに作用する正味の力はゼロです。 これをランプに平行な力に適用します。
* σf_parallel=0
* f -mg sin(25°)=0
4。適用力(f)を解決します
* f =mg sin(25°)
* f =(125.0 kg)(9.8 m/s²)(sin 25°)
* f≈519.5n
したがって、適用された力fの大きさは約519.5ニュートンです。