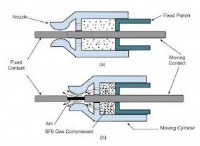
これが故障です:
特性:
* 独立: それらは他の量から派生していません。
派生量の基礎: 他のすべての物理量は、基本量の組み合わせを使用して定義できます。
* ユニバーサル: それらの定義と値は、測定システムに関係なく同じです。
基本的な物理量の例:
* 長さ: 2つのポイント間の距離を表します。メーター(m)、センチメートル(cm)などのユニットで測定します。
* 質量: オブジェクト内の物質の量を表します。キログラム(kg)、グラム(g)などのユニットで測定します。
* 時間: イベントの期間を表します。秒、数分(分)などのユニットで測定。
* 温度: システムの暑さまたは寒さの程度を表します。摂氏(°C)、華氏(°F)、ケルビン(k)などのユニットで測定されます。
* 電流: 電荷の流れを表します。アンペア(A)などのユニットで測定。
* 物質の量: 物質のエンティティ(原子、分子など)の数を表します。モール(mol)などの単位で測定。
* 明るい強度: 特定の方向に光源によって放出される電力を表します。 Candela(CD)などのユニットで測定。
派生量:
派生量は、基本量の組み合わせを使用して定義されます。例は次のとおりです。
* 速度: 単位時間(長さ/時間)あたり移動する距離
* 力: 質量時間加速(質量 *長さ/時間²)
* 密度: 単位体積あたりの質量(質量/長さ³)
* エネルギー: 力時間距離(質量 *長さ²/時間²)
基本量の重要性:
基本的な量を理解することは重要です。
* 測定値の一貫性: 定義された一連の基本量セットを使用すると、さまざまな科学分野で測定の均一性が保証されます。
* 単位の一貫したシステムの構築: 基本量は、派生ユニットを定義するための基礎を提供し、物理的特性を測定するための凝集システムを作成します。
* 複雑な現象を単純化: 基本量の観点から複雑な物理現象を表現することにより、それらをよりよく理解し、モデル化することができます。
要約すると、基本的な物理量は物理学の構成要素であり、他のすべての量を定義および測定するための基盤として機能します。彼らの独立性と普遍性は、物理的な世界を包括的に理解するためにそれらを不可欠にします。