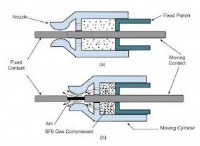
セットアップの理解
* ボール: 垂直にぶら下がっている質量 'm'。
* 文字列: ボールをプーリーに接続する明るい弦は、質量がなく、依存しないと想定されています。
* プーリー: 慣性モーメント(I)と半径(R)を備えた均一な固体ディスク。
* 摩擦のない車軸: プーリーは、摩擦損失なしに自由に回転します。
重要な概念
* エネルギーの保存: システムの総機械エネルギー(ボールとプーリー)は一定のままです。これは、ポテンシャルエネルギー、ボールの運動エネルギー、およびプーリーの回転運動エネルギーの合計が一定であることを意味します。
* 回転運動: プーリーは、弦の張力によって生成されるトルクのために角度加速度を経験します。
* トルク: 弦の張力はプーリーにトルクを作成し、それを回転させます。
* 慣性モーメント: オブジェクトが回転運動の変化にどれほど耐性であるかの尺度。固体ディスクの場合、i =(1/2)MR²。
方程式を導出する
1。ボールに作用する力:
*重力:MG(下向き)
*文字列の張力:t(上向き)
2。滑車に作用する力:
*弦の張力:t(接線力)
3。ボールの運動方程式:
*ニュートンの第二法則:ma =mg -t
*ボールの加速:a =(g -t/m)
4。プーリーの運動方程式:
*トルク:τ=tr
*角度加速:α=τ/i =(tr)/(1/2mr²)=(2t/mr)
*線形加速度(A)と角加速度(α)の関係:A =Rα
5。エネルギーの保存:
*ボールの初期ポテンシャルエネルギー:MGH(ここで、「H」は初期の高さです)
*ボールの最終的なポテンシャルエネルギー:0(ボールが底に到達したとき)
*ボールの運動エネルギー:(1/2)mV²
*プーリーの回転運動エネルギー:(1/2)iω²=(1/4)MR²ω²
6。線形および角速度の関連:
* v =rω
問題の解決
1。張力を解決する(t):
*ボールの運動方程式から「a」の式を、線形加速度と角度加速度(a =Rα)の関係に置き換えます。
* t =(2/3)mgが見つかります
2。加速度(a):を見つけます
* Tの値をボールの運動方程式に置き換えます(Ma =mg -t)。
* a =(1/3)gを取得します
3。角度加速度(α)を計算します:
*方程式α=(2T/MR)を使用し、Tの値を置き換えます。
4。ボールの速度(v)を決定します:
*エネルギー方程式の保存を使用し、「V」を解きます。
キーポイント
*弦の張力は、プーリーの回転慣性によるボールの重量よりも少ない。
*プーリーの回転が遅くなるため、ボールの加速は「G」よりも少ない。
*ボールが落ちるにつれて失われたエネルギーは、プーリーの回転運動エネルギーに移されます。
特定の質問があるか、これらの値のいずれかを計算したいかどうかを教えてください。必要に応じて、より詳細な計算を提供できます。