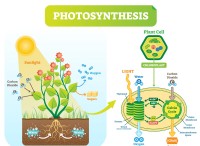
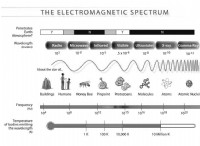
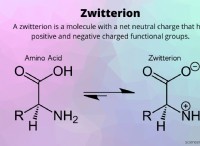
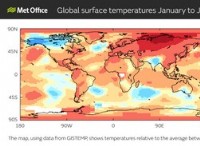
中心力は速度の正方形に直接比例します:
* 速度の増加: 円内で移動するオブジェクトの速度が増加すると、そのパスを維持するために必要な中心力も に増加します 。 これは、高速では、オブジェクトが(慣性のため)より直線で移動したいと考えているため、その経路を曲がるために強力な力が必要であることを意味するためです。
* 速度の低下: 逆に、速度が低下すると、必要な中心力も減少します。
数学的関係:
中心力(FC)、質量(M)、速度(V)、および円形経路の半径(R)の関係は、次の方程式で与えられます。
`` `
fc =(mv^2) / r
`` `
この方程式は、中心力が速度の平方に直接比例することを明確に示しています(v^2)。
例:
* 角を曲がる車: 高速で走行する車は、滑らずに角を曲がるために、より大きな中心力を必要とします。これが、鋭い角を曲がるときに減速する必要がある理由です。
* 軌道の衛星: 衛星軌道地球は、軌道を高速で維持するために、より大きな中心力を必要とします。
* 弦の上でボールを振る: 弦の上でボールを速くスイングするほど、ボールを輪になった状態に保つために、ひもに及ぼす力が大きくなります。
要約:
高速では、円の動きを維持するために、比例的にはるかに大きな中心性力が必要です。これは、オブジェクトが円形の経路でどのように移動するかを理解する上で重要な概念です。