Lateral Displacement (d) =t * sin(i - r) / cos(r)
どこ:
* d 横方向の変位です
* t ガラススラブの厚さです
* i 入射角です
* r 屈折の角度です
派生:
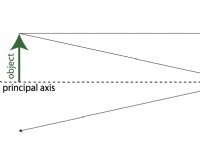
1。ガラススラブ上の角度「i」で通常の光線を考慮してください。
2。光線は最初のインターフェイスで屈折し、通常の(Snellの法則に従って)角度「R」でスラブに入ります。
3。レイはスラブを通り抜け、角度「r」を通常のものと維持します。
4。光線は2番目のインターフェイスで再び屈折し、入射光線に平行なスラブから出現しますが、距離「d」によって横方向に置かれます。
式を導き出すために、状況のジオメトリを検討します:
1。横方向の変位 'd'は、出現光線と入射光線の投影経路との間の距離です。
2。この距離は、入射光線、緊急光線、およびスラブを通る光線の経路によって形成される右角の三角形を考慮することで見つけることができます。
3。この三角形のベースの長さは「t」(スラブの厚さ)です。
4。ベースとは反対の角度は(i -r)。
5。ベースに隣接する角度は「r」です。
したがって、三角法を使用:
* sin(i -r)=d / hypotenuse
* cos(r)=t / hypotenuse
'd'を解決すると、式:が与えられます
d =t * sin(i -r) / cos(r)
注:
*横方向の変位は、スラブの厚さと、入射角と屈折角の違いの正弦に直接比例します。
*横方向の変位は、屈折角のコサインに反比例します。
*入射光線がスラブの表面に垂直である場合、横方向の変位はゼロになります(i =0)。
*入射角が臨界角に等しい場合、横方向の変位は最大になります。