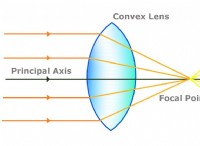
その理由は次のとおりです。
* 運動の最初の方程式:
* 式: v =u + at
* 説明: この方程式は、オブジェクトの最終速度(v)を初期速度(u)、加速(a)、および時間(t)に関連付けます。一定期間にわたって速度の *変化 *に焦点を当てています。
* 動きの2番目の方程式:
* 式: S =UT +(1/2)AT²
* 説明: この方程式は、オブジェクトの変位を初期速度(u)、加速(a)、および時間(t)に関連付けます。動き中に移動した *距離 *に焦点を当てています。
関係:
2番目の運動方程式は、運動の最初の方程式から導き出されます。 このように考えてください:
1。積分速度: 最初の方程式は、速度が時間とともにどのように変化するかを示します。この方程式を統合すると(速度時間グラフの下の領域を見つけます)、変位が取得されます。この統合プロセスは、(1/2)AT²の用語がどこから来たのかです。
なぜ「減らす」ことができないのか
次のために、2番目の方程式を単純に「減らす」ことはできません。
* 異なる変数: 2番目の方程式には、最初の方程式がそうではない変位が含まれます。
* さまざまな概念: 2番目の方程式は、移動した *総距離 *を説明し、最初の方程式は *速度 *の変化に焦点を当てています。
要約:
運動の第1および2番目の方程式は相互接続されており、2番目の方程式は最初の方向から派生しています。それらは、動きに関する異なるが補完的な情報を提供します。