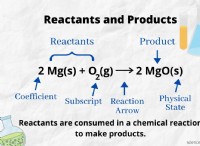
ここに:
* 派生: キネマティック方程式は、Calculus、特に統合を使用して導出されます。 統合は、一定の値を扱うときにスムーズに機能します。 加速が一定ではない場合、統合はより複雑になります。
* 瞬時値: 運動学的方程式は、一定期間にわたる速度と加速度の平均値で動作します。加速度が変化する場合、平均値は、特定の瞬間に瞬間値を表すものではない場合があります。
加速が一定ではない場合に何をするか:
1。計算: 計算を使用して問題を解決します。これには、加速度関数を統合して速度を取得し、速度を統合して変位を取得することが含まれます。
2。数値的方法: Eulerの方法やRunge-Kuttaメソッドなどの数値的方法を使用して、加速度が一定ではない場合の動きを近似できます。
3。グラフィカル分析: 加速時間グラフが提供されている場合、曲線の下の面積は速度の変化を表します。
重要な注意:
運動学的方程式は、短い時間間隔の運動を分析するためにまだ使用できます ここで、加速度はほぼ一定です。ただし、注意し、一定の加速の仮定が検討中の特定の時間枠内で有効であることを確認する必要があります。