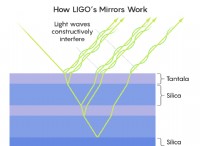
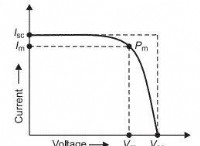
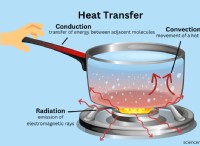
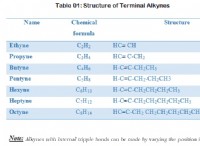
`` `
m =m₀ /√(1 -v² /c²)
`` `
どこ:
* m 相対論的質量です
* m₀ 残りの質量です(安静時の物体の質量)
* v オブジェクトの速度です
* c 光の速度です
v として アプローチ c 、方程式の分母はゼロに近づきます。これは、相対論的質量 m を意味します 無限に近づきます。
したがって、理論的には、光の速度で移動するオブジェクトの質量は無限になります。
ただし、次のことに注意することが重要です。
* 質量のあるオブジェクトが光の速度に達することは不可能です。 これは、オブジェクトの速度が光の速度に近づくと、そのエネルギー要件が無限になるためです。
*相対論的質量の概念は現在、現代の物理学で時代遅れと見なされています。 代わりに、物理学者はオブジェクトのエネルギーに焦点を合わせます 速度が上がるにつれて。
したがって、方程式は光の速度で無限の質量を示唆していますが、実際のオブジェクトには適用されない理論的な結果です。