1。 説明と定量化:
* 測定: 科学は正確な測定に大きく依存しています。数学は、現象(長さ、質量、時間、温度など)を定量化するためのツールを提供します。
* データ分析: 科学者はデータを収集し、数学は彼らがそれを分析するのに役立ちます。彼らは統計を使用して、データ内のパターン、傾向、および関係を見つけます。
* モデリング: 数学により、実際のシステムを表すモデルを作成できます。これらのモデルは、数学的方程式、コンピューターシミュレーション、またはその他の表現です。
2。 予測と説明:
* 処方理論: 多くの科学理論は、数学的方程式に基づいています。たとえば、ニュートンの普遍的重力の法則は、物体間の重力を表す数学的方程式です。
* 予測の作成: 数学により、科学者はシステムの振る舞いについて予測することができます。 これは、天気予報、天文学、工学などの分野で重要です。
* 現象の説明: 数学モデルは、科学者が自然現象を促進する根本的なメカニズムを理解するのに役立ちます。
3。 実験とテスト:
* 実験の設計: 数学は、実験を設計し、データを収集するための最良の方法を決定するために使用されます。
* 結果の分析: 数学は、実験の結果を分析して結論を引き出し、仮説をテストするのに役立ちます。
科学における数学の例:
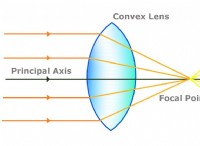
* 物理学: ニュートンの動きの法則、アインシュタインの相対性理論、量子力学、および電磁気はすべて数学的方程式に基づいています。
* 化学: 化学反応は、反応物と生成物の定量的関係を扱う数学の分岐である化学量論を使用して説明されています。
* 生物学: 人口のダイナミクス、遺伝学、および疾患の発生の研究には、しばしば複雑な数学モデルが含まれます。
* 天文学: 惑星の軌道、星形成、宇宙の拡大に関連する計算は、数学に大きく依存しています。
要するに 数学は科学の基礎です。科学的アイデアを説明、定量化、予測、説明、テストするためのツールを提供します。