* 寸法正確性: これは、方程式の両側のユニットが一致することを意味します。たとえば、「距離=速度x時間」のような方程式は、長さの単位(メートルなど)、長さの単位単位(1秒あたりのメートル)、および時間単位(秒など)での速度で測定されるため、寸法的に正しいです。
* 物理的関係: これは、実際の現象を正確に記述する方程式を指します。それは物理的原則に基づいて、実験的に検証する必要があります。
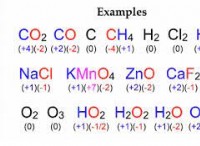
例:
* 寸法的に正しいが物理的ではない: 方程式「距離=速度x時間」を考慮してください。この方程式は寸法的に正しいですが、実際の物理現象は説明していません。距離が速度と時間の平方に比例するという既知の関係はありません。
* 物理的な関係と寸法正しい: 方程式「F =MA」(ニュートンの動きの第二法則)は、次元的に正しく、物理的な関係の両方です。力(f)は、ニュートンで、質量(m)でキログラムで測定され、加速度(a)が1秒あたりの2乗で測定されます。方程式は、現実世界の力、質量、加速の関係を正確に表します。
要約:
寸法正確性は物理的な関係に必要な条件ですが、それだけでは十分ではありません。方程式は、実際の物理現象を表すことなく、寸法的に正しいことができます。 物理的な関係になるには、方程式は物理法則に基づいており、実験的に検証されている必要があります。