定常状態近似|化学

コアコンセプト

この記事では、連続反応の動力学を理解する上で重要なツールである定常状態近似について学びます。

定常状態近似を使用しない連続反応動力学

定常状態近似は、連続反応メカニズムをモデル化する数学を単純化するための便利なツールです。化学反応速度論では、連続反応は単純な反応速度論を持っているように見えるかもしれませんが、多くの場合、頭痛を誘発する数学が含まれます。次の連続した反応を取ります:

A→B→C

分子 A は B に変換され、B は C に変換されます。速度定数 k_a そしてk_b それぞれ、最初と 2 番目の反応の速度を通知します。各反応は単分子であるため、反応における各種の変化率を簡単に見つけることができます:

-k_a [A] =(d[A])/t

k_a [A]-k_b [B] =(d[B])/t

(d[C])/t =k_b [B]

一次速度法則を使用して、時間の経過に伴う A の濃度をモデル化する方程式も見つけることができます。

[A] =[A]₀ e

次に、この率の法則を B の変化率に代入できます:

(d[B])/t+k_b [B] =k_a [A]₀ e

B の初期濃度がないと仮定すると、この微分方程式を解くことができます ([B]₀ =0) そしてその k_a ≠ k_b :

[B] =(e-e)k_a /(k_a -k_b )

最後に、C の初期濃度がなかったと仮定すると ([C]₀ =0, [A] + [B] + [C] =[A]₀ )、時間の経過に伴う C の濃度の方程式を取得します。

[C] =[A]₀ (1+(k_a e-k_b e)/(k_b -k_a ))

おわかりのように、一次反応速度論のかなり単純な概念を使用すると、連続反応の計算は急速に複雑になります。 2 ステップを超える反応を考慮すると、計算が難しくなります。ここで、定常状態近似が役立ちます。

単分子動力学の定常状態近似

定常状態の近似では、中間化合物である分子 B の濃度の変化は、無視できない場合でも、どの時点でも常に非常に低いままであると考えられます。

(d[B])/t ≈ 0

この概算を行うには、連続反応系が 2 つの多くの場合正しい基準を満たす必要があります。

一般的に、B の濃度は A または C に比べてはるかに低いままです。
A が反応して B を形成する速度は、B が反応して C を形成する速度よりもはるかに遅いです。これは、A が B を形成することが速度決定ステップであることを意味します。

多くの連続反応システムがこれらの基準を満たしています。多くの場合、B は不安定な中間体として振る舞い、特定の低いしきい値に達するまで濃度が上昇します。次に、生成された追加の B は、その不安定性のために、B の生成よりもはるかに速く C に急速に変換されます。数学的には、これは kb が ka よりもはるかに高い量を表すことを意味します。

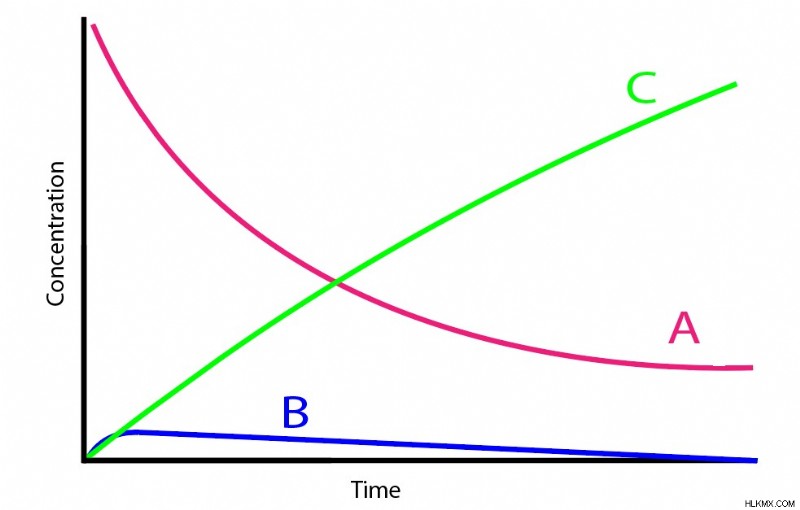
両方の基準が満たされると、定常状態の近似によって数学が大幅に簡素化されます。つまり、A と B の濃度を直接関連付ける方法が得られます。

0 =(d[B])/t =k_a [A] – k_b [B]

(k_a /k_b )[A] =[B]

これにより、時間の関数としての C 濃度の式をより簡単に導き出すことができます。

[A]₀ =[A] + [B] + [C]

[C] =[A]₀ – [A] – [B]

[C] =[A]₀ – [A] – (k_a /k_b )[A]

次に、A の変化に関する 1 次レートの法則を実装して、最終的に C を時間で表現します。

[C] =[A]₀ – ([A]₀ e) – ((k_a /k_b )[A]₀ e)

[C] =[A]₀ (1 – e – (k_a /k_b )e)

多くの場合、k_a の場合、方程式をさらに単純化できます。 k_b に比べて無視できる (k_a /k_b ≒0）。これにより、括弧内の第 3 項を無視することができ、以下が得られます:

[C] =[A]₀ (1 – e)

酵素動態の定常状態近似

単分子動力学に加えて、定常状態近似は、より複雑な連続反応で役立ちます。非単分子反応における近似の最も重要な適用には、酵素触媒作用のミカエリス-メンテン速度論が含まれます。一般的な酵素触媒反応では、基質 (S) が酵素 (E) に可逆的に結合し、酵素-基質複合体 (ES) を形成します。次に、酵素は生成物 (P) の形成を触媒し、複合体から放出します:

E + S ⇌ ES → E + P

以前の単分子反応とは異なり、この反応には 3 つの合計速度定数が含まれます。 k₁ k_-1 は、複合体を形成する酵素と基質の転送速度を表します。逆反応について説明します。 k₂ 生成物の形成と複合体からの酵素の再生に関連しています。数学を単純化するために、定常状態の近似と、平衡に関連する別の有用な近似を実装することがよくあります。

定常状態と酵素の関係

生物学的システムと工業的アプリケーションの両方で、基質は酵素よりもはるかに過剰に存在する傾向があります。酵素濃度が低いと複合体の形成が制限されるため、これは「中間体の低濃度」条件を満たします。高濃度の基質は本質的にすべての酵素を基質で飽和させる必要があるため、これだけで酵素複合体の定常状態を仮定することができます。これにより、酵素-基質複合体の濃度が反応の間一定に保たれます:

(d[ES])/t =0

簡略化された数学

複合体の濃度の変化を表すために、最初の反応の前進速度から逆速度を引いたものと、2 番目の反応の前進速度を使用します。重要なことに、これらの各レートは、1 次および 2 次レートの法則を使用して導き出すことができます。次に、定常状態の近似を使用して 3 つのレートを関連付けることができます。

(d[ES])/t =0 =k₁ [E][S] – k_-1 [ES] – k₂ [ES]

k₁ [E][S] =k_-1 [ES] + k₂ [ES]

次に、並べ替えて次の式を得ることができます:

([E][S])/([ES]) =(k_-1 + k₂ )/k₁

この時点で、[E] と [ES] は数学的に互いに関連していることを覚えておく必要があります。具体的には、それらの追加により、使用済みおよび未使用の酵素の総濃度が得られます。

[E]_合計 =[E] + [ES]

ここで、[E]_total を [E] に置き換えます。 -[ES]:

(([E]_合計 -[ES])[S])/([ES]) =(k_-1 + k₂ )/k_-1

右側の式は、化学者がミカエリス定数と呼ぶものに等しい.この値は、酵素とその基質との親和性を特徴付けるのに使用されます。ミカエリス定数が高いほど親和性が低く、親和性が高い酵素-基質ペアは定数が低くなります。

KM =(k_-1 + k₂ )/k₁

ミカエリス定数を前の方程式に代入すると、[ES] を解くことができます。

(([E]_合計 – [ES])[S])/([ES]) =KM

[ES] =([E]_合計 [S])/(KM + [S])

最後に、この表現を製品形成率に置き換えることができます。この方程式は、酵素反応の初速度として機能します。

v₀ =(d[P])/t =k₂ [ES]

v₀ =(k₂ [E]_合計 [S])/(KM +[S])

したがって、定常状態近似のおかげで、酵素反応速度論を研究する生化学者にとって重要なパラメーターである反応の初速度を導き出すことができます。