ソーラー ジェットは、垂直またはわずかに斜めの磁力線に沿って流れる高温プラズマの小規模な噴火です。それらは、光球から外側のコロナまでの太陽大気に遍在しています。ソーラー ジェットは常に、磁気エネルギーを熱と運動エネルギーに変換するマイクロ フレアに関連付けられています。
ジェットの発生率は太陽大気で非常に高く、コロナプラズマを加熱し、高速太陽風を加速するための有力な候補源と見なすことができます。回転する竜巻のような太陽ジェットは、太陽大気で最も壮観なイベントの 1 つです。コロナ ホール領域でのさまざまな機器による最初の観測以来、Solar Dynamics Observatory の高解像度データによって、これらの太陽ジェットの物理を理解するための非常に目覚ましい進歩が遂げられました。 (SDO ) 宇宙船。
一般に、ソーラー ジェットは、いわゆるケルビン ヘルムホルツ不安定性 (KHI) に対して不安定になる電磁流体力学 (MHD) 波の伝播をサポートします。異なる速度の流体が同じ方向に流れる場合、2 つの異なる速度の境界領域付近で強い速度せん断が発生することは、長い間知られていました。この速度せん断は、KHI の発生を示す境界で渦シートを生成します。
SDO に搭載された Atmospheric Imaging Assembly (AIA) からの多波長データの使用 、チェンらは、太陽の北極近くのコロナホールで発生する回転ジェットを研究しました。上の図に示されている AIA 304 Å 画像 (ムービーも参照) は、ジェットの詳細な進化を示しています (Zhelyazkov et al.)。白い矢印で示されているように、ジェットの右側の境界にある小さな移動ブロブは、KHI によって生成される可能性があります。ブロブの速度は 120 ± 8 km/s であることが判明しましたが、初期不安定段階での時間的進化は約 2 ~ 4 分であることが判明しました。
この回転するソーラー ジェットは、速度 U で垂直に移動するものとしてモデル化できます。 半径 a の弱くねじれた磁束チューブ =9.8 × 10 km、電子数密度 n ジェット =1.0 × 10 cm、温度 T ジェット =1.6 MK、n の静的コロナ プラズマに囲まれている cor =0.9 × 10 cm、T cor =1.0 MK、および 3 G の磁場。円柱座標 (r , φ 、z )、ねじれたジェット磁場は B で与えられます =(0, Bφ (r )、Bz )。回転速度も同様に U として表されます =(0, Uφ (r )、Uz )。磁場と流速のねじれは、パラメータ ε によって特徴付けられます。 1 =Bφ /Bz そしてε 2 =Uφ /Uz 、それぞれ、方位成分 Bφ そしてUφ 管表面で評価される r =a .測定された Uz で =114 km/s と Uφ =136 km/s、ε 2 =1.2.
MHD モードの伝搬は、密度コントラスト η に大きく依存します。 、ジェットとその環境の間。 η の定義 nとして cor /(n ジェット + n cor )、η =0.474。もう 1 つの重要なパラメータは、軸方向の磁場成分 b の比率です。 、外部から内部へ(この場合は b =1.21)、ジェット内のアルフベン速度、v あ ≒150km/s。波の伝播に関連するすべての摂動が exp[i(–ωt + mφ + kz z )]、ここで ω 角波周波数、m 方位角モード番号、および kz 軸波数、MHD 波動伝搬がいわゆる分散関係 D によって支配されていることを示すことができます (ω 、分 , kz 、a , η 、b , ε 1 , ε 2 、Uz 、v あ ) =0、ここで、不安定条件を検索する際に、波の周波数を複雑な量と見なします:ω =ω + iγ .
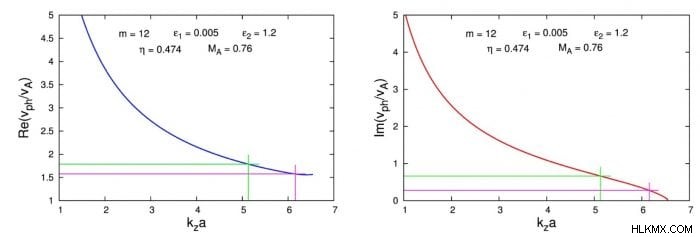
上記の分散方程式の解は、アルフベン速度波の位相速度 v に関して正規化された の依存関係として求められました。 ph /v あ =ω /(kz v あ ) 正規化された波数 kz について .波の周波数は複素数であると仮定するので、kz の 2 つの関数のペアを取得する必要があります。 :Re(v の 1 つ ph /v あ ) と Im(v の別の ph /v あ )。 KHI が登録された軸ジェット速度 Uz で発生すると仮定します =114 km/s、v に関して正規化 あ アルフベン マッハ数 M を生成します あ =0.76.
ジェット磁場のねじれに関しては、比較的小さいもの、つまり ε を選択しました。 1 =0.005。これらの入力パラメータの下で、前述の η の値とともに 、b 、および ε 2 、分散方程式の数値解析は、1D kz に有限サイズの不安定領域が存在することを示しています -スペース。このような不安定ウィンドウの幅と位置は、主にモード番号 m に依存します。 .不安定な MHD モードの波長を予想すると、λ KH 、約 10 ~ 12 mm (ジェットのほぼ半幅) になると、そのような KHI は m で発生する可能性があります。 =12. 上記の依存関係は、図 1 にグラフで示されています。
固定された 2 つの不安定な波長での無次元波の位相速度と成長率から、対応する周波数成長率 γ を絶対単位で見つけます。 KH 、および不安定性の成長/進化時間 τ KH =2π /γ KH 、および波の位相速度:
λ KH =10ミリ ⇒ γ KH =26 × 10 秒; τ KH ≈ 4 分; v ph ≈ 236 km/s
λ KH =12ミリ ⇒ γ KH =52 × 10 秒; τ KH ≈ 2 分; v ph ≈ 267 km/s
両方の波長の KHI の発生の評価された時間間隔は τ であることに注意してください。 KH ≈ 4 分と ≈2 分であり、これは初期段階におけるブロブの観測的に発見された時間的進化時間と一致します。
計算によると、不安定性ウィンドウの幅は、磁場ツイスト パラメーター ε の増加とともに狭くなります。 1 —実際には、不安定範囲の右側の限界が左側にシフトします。ただし、これは、一般に、不安定な波長がより長くなり、いくつかの臨界 ε になることを意味します。 1 ジェットの高さ H に等しい最短波長が展開されます =179 mm。臨界 ε よりも大きな磁場ツイストの場合 1 波動現象についてはまったく語れません。したがって、固定された左側の制限 (kz )lhs 式 (kz )lhs ≡ 2πa /へ =0.344。 ε の増加に伴って不安定範囲が狭くなるこのプロセス 1 図 2 の右側のパネルに明確に示されています。
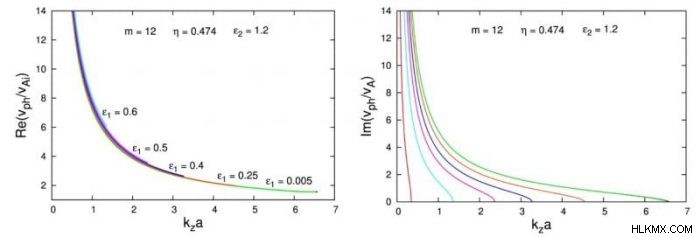
そこの赤い曲線は kz で取得されます =0.344 で、この ε の値 1 不安定ウィンドウの幅はゼロです。一方、ε の定義から 1 、方位磁場が不安定性の開始を抑制することになります。 Bz で =2.45 G で、方位磁場は ≈1.7 G です。したがって、磁場のねじれが強すぎない場合、タイトルで提起された質問に対する答えは「はい」です。そうでなければ、1.7 G という十分に大きな方位磁場成分が KHI の発生を抑制することができます。
これらの調査結果は、SDO/AIA によって観測されたねじれ太陽極コロナ ホール ジェットにおけるケルビン-ヘルムホルツ不安定性というタイトルの記事で説明されており、最近、ジャーナル Advances in Space Research に掲載されました。この作業は、Ivan Zhelyazkov (ソフィア大学)、Teimuraz Zaqarashvili (グラーツ大学)、Leon Ofman (NASA ゴダード宇宙飛行センター)、および Ramesh Chandra (Kumaun 大学) によって実施されました。