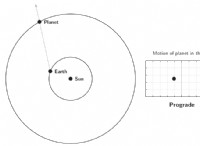
* 太陽に近い惑星はより速く移動します。
* 太陽から遠く離れた惑星は遅くなります。
この関係は、ケプラーの惑星運動の第三法則によって説明されています 。この法律では、惑星の軌道の平方(太陽の周りの1つの軌道を完成させるのにかかる時間)は、太陽からの平均距離の立方体に比例していると述べています。
より詳細な説明を次に示します。
* エネルギーの保存: 惑星の総エネルギー(運動 +電位)は、軌道全体で一定のままです。 惑星が太陽に近づくと、その重力ポテンシャルエネルギーが減少します(巨大な太陽に近いため)。総エネルギーを節約するには、その運動エネルギー(したがって速度)が増加する必要があります。
* 角運動量: 惑星も角運動量を節約します。 惑星が太陽に近づくと、軌道の半径が減少します。 一定の角運動量を維持するには、その速度を上げる必要があります。
簡単に言えば:
惑星を回転するトップと考えてください。上部がスピンの中心に近づくほど、回転する速度が速くなります。同じ概念が太陽を周回する惑星にも当てはまります。
重要な注意: 惑星の速度は軌道全体で一定ではありませんが(太陽に最も近い地点で最も速く、近日点と呼ばれ、アフェリオンと呼ばれる最も遅いポイント)、平均速度 太陽からの距離に反比例する。