主な違い – ヘキサゴン vs 単斜晶ユニットセル
六角形および単斜晶単位セルという用語は、結晶系に関連しています。結晶系は、結晶軸の可能な関係に従って分類された 7 つのカテゴリ (立方晶、正方晶、斜方晶、三方晶、六方晶、単斜晶、および三斜晶) のそれぞれです。結晶系の単位格子は、結晶系の繰り返しパターンを表す構造の一部です。代表的な原子とそれらの原子の繰り返し配置で構成されています。単位格子は立体構造であり、結晶系はそれぞれ独自の単位格子構造を持っています。単位セルは箱です。さまざまなユニークなパターンで配置された原子が含まれています。この単位セルは、単位セルのエッジと角度の間の長さである格子定数に関して記述されます。六角形ユニット セルと単斜晶ユニット セルの主な違いは、六角形ユニット セルの 3 つの軸のうち 2 つが同じ長さであるのに対し、単斜晶ユニット セルでは 3 つの軸の長さが等しくないことです。
対象となる主な分野
1.単位セルとは
– 説明
2.ヘキサゴンユニットセルとは
– 定義、構造、独自の機能
3.単斜晶系ユニットセルとは
– 定義、構造、独自の機能
4.六角形と単斜晶の単位セルの違いは何ですか
– 主な違いの比較
重要な用語:結晶系、六角形、格子パラメーター、単斜晶系、単位セル

ユニットセルとは
単位セルは、結晶系の繰り返しパターンを表す小さな構造です。ボックス構造です。このボックスには、材料に存在するすべてのタイプの原子が含まれています。これは 3D 構造です。単位セルは、格子定数を使用して記述されます。格子は、金属または他の結晶性固体内の原子、イオン、または分子の規則的に繰り返される 3 次元配置です。格子パラメータは、単位セルのエッジと角度の間の長さです。長さ (軸とも呼ばれます) は記号 a、b、c で与えられ、角度はアルファ (α)、ベータ (β)、ガンマ (γ) で与えられます。
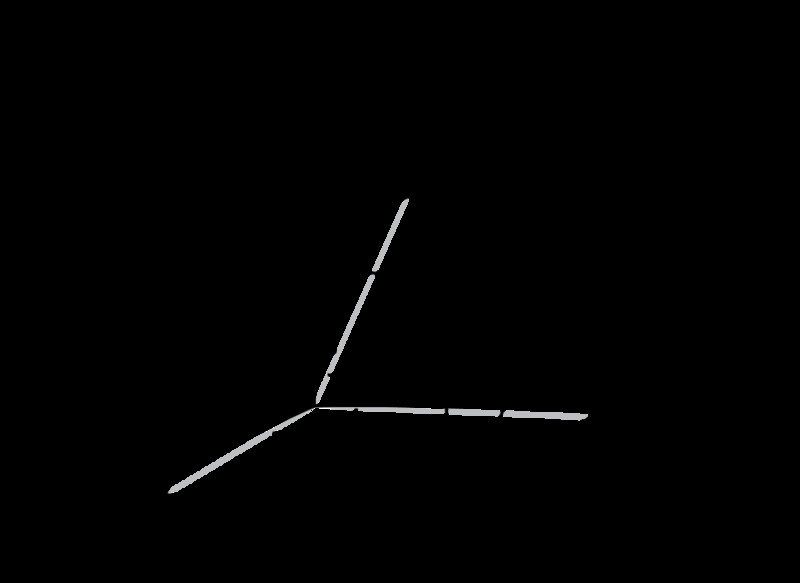
図 1:単位セルの格子パラメータ
セル内の原子の位置は、X、Y、Z で指定された原子位置によって記述されます。これらの点は、参照格子構造から測定されます。
ヘキサゴン ユニット セルとは
ヘキサゴン ユニット セルは、六方晶系のユニット セルです。六角形の結晶構造を持つ材料の原子の配置を表します。長さが同じ 2 つの軸と、長さが異なる 1 つの軸があります。この軸は、他の 2 つの軸に対して垂直です。 2 つの類似した軸の間の角度は 120 です。
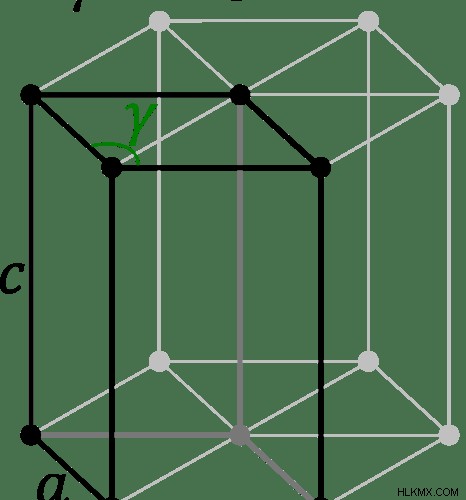
図 2:六角形のユニット セル
簡単に言えば、六角形ユニットセルの特定の機能は次のとおりです。
- a=b≠c
- α=β=90
- γ=120.
単斜晶系ユニット セルとは
単斜晶単位胞は、単斜晶系の単位胞です。単斜晶構造を持つ物質の原子の配列を表します。単位セルの 3 つの軸 (a、b、c) は等しくありません。単斜晶ユニットは、平行四辺形を底辺とする長方形の形状をしています。平行四辺形は、2 組の平行な辺を持つ単純な構造です。したがって、2 つの軸は 90 度の角度で互いに交わります。
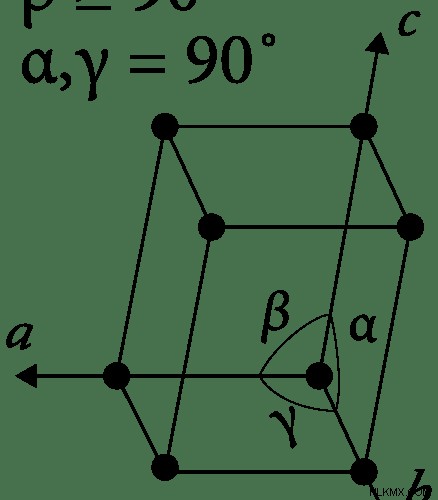
図 3:単斜晶系ユニット セル
簡単に言うと、六角形ユニットセルの特徴は次のとおりです:
- a≠b≠c
- α=γ =90
- β≠90
Hexagon と Monoclinic Unit Cell の違い
定義
六角形 ユニット セル: ヘキサゴン ユニット セルは、六方晶系のユニット セルです。
単斜晶ユニットセル: Monoclinic unit cell は、単斜晶系の単位胞です。
軸の長さ
六角形 ユニット セル: 六角形の単位格子には、長さが似ている 2 つの軸と、長さが異なる 1 つの軸があります (a=b≠c)。
単斜晶ユニットセル: 単斜晶の単位セルには、長さが等しくない 3 つの軸があります (a≠b≠c)。
角度
六角形 ユニット セル: 六角形の単位格子は、α と β の角度が 90° に等しく、γ の角度が 120° です。
単斜晶ユニットセル: 単斜晶の単位セルは、α と γ の角度が 90° に等しく、β は 90° に等しくありません。
平行四辺形の存在
六角形 ユニット セル: 六角形ユニット セルには、ユニット セルに平行四辺形構造がありません。
単斜晶ユニットセル: 単斜晶ユニットセルは、ユニットセルのベースとして平行四辺形構造を持っています。
結論
六角形および単斜晶の単位格子は、結晶系の原子配列の繰り返しパターンを表す結晶系の一部です。六角形ユニット セルと単斜晶ユニット セルの主な違いは、六角形ユニット セルには同じ長さの 2 つの軸があるのに対し、単斜晶ユニット セルには長さが等しくない 3 つの軸があることです。