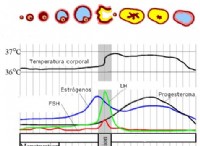
特殊相対性理論は、時間に関する興味深い概念を導入しました。参照フレームを移動する場合、時間は同じ速度で経過しません。動いている時計は、静止した座標系の時計よりも遅く動きます。この効果は、時間の遅れとして知られています。この時間差を計算するために、ローレンツ変換が使用されます。
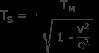
どこ
TM は、移動参照フレームで測定された持続時間です。
TS は静止座標系から測定された時間です。
v は、基準の移動フレームの速度です
cは光速
時間の遅れの例題
この効果が実験的に証明された 1 つの方法は、高エネルギー ミューオンの寿命を測定することでした。ミューオン(記号μ)は不安定な素粒子で、電子とニュートリノ2つに崩壊するまでに平均2.2マイクロ秒存在します。ミュー粒子は、宇宙線放射が大気と相互作用するときに自然に形成されます。それらは、存在時間を正確に測定できる粒子コライダー実験の副産物として生成される可能性があります。
実験室でミュオンを作り、8.8μsec存在することを観測。ミューオンの移動速度は?
解決策
ミューオンの座標系から、2.2 マイクロ秒存在します。これは TM です 私たちの方程式の値。
TS は、8.8 マイクロ秒の静的基準系 (実験室) から測定された時間、または存在する必要がある長さの 4 倍です:TS =4 TM .
速度について解きたいので、方程式を少し単純化しましょう。まず両辺を TM で割ります .
方程式をひっくり返す
部首を取り除くために両側を四角にします。
このフォームの方が作業が簡単です。 TS を使用 =4 TM 得る関係
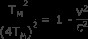
また
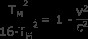
TM をキャンセル 去る
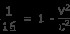
両辺から 1 を引く
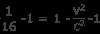
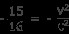
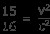
両辺にcを掛ける
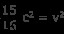
両辺の平方根を取ると v
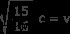
v =0.968c
答え:
ミューオンは光速の 96.8% で動いていました。
この種の問題に関する重要な注意事項の 1 つは、速度が光速の数桁以内でなければ、測定可能で顕著な違いが生じないことです。