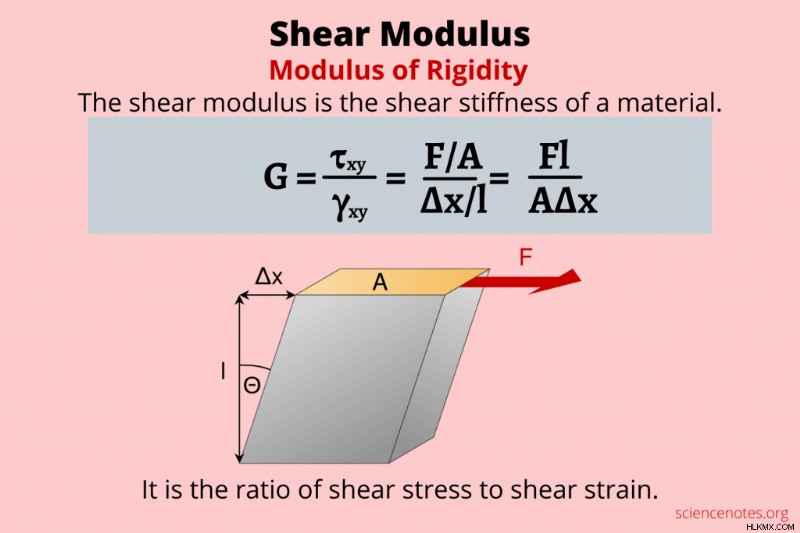
定義上、せん断弾性率 材料のせん断剛性で、せん断応力とせん断ひずみの比率です。せん断弾性率の別名は、剛性率です。せん断弾性率の最も一般的な記号は大文字の G です。その他の記号は S または μ です。 .
- せん断弾性率の高い材料は剛体です。変形させるには大きな力が必要です。
- せん断弾性率の低い材料は柔らかい固体です。ごくわずかな力で変形します。
- 流体の定義の 1 つは、せん断弾性率がゼロの物質であるというものです。どんな力でも変形します。したがって、液体または気体のせん断係数はゼロです。
せん断弾性率の単位
せん断弾性率の SI 単位は、圧力単位パスカル (Pa) です。ただし、パスカルは 1 平方メートルあたりのニュートン (N/m) であるため、この単位も使用されます。その他の一般的な単位は、ギガパスカル (GPa)、ポンド/平方インチ (psi)、キロポンド/平方インチ (ksi) です。
せん断弾性率の式
せん断弾性率の式はさまざまな形式を取ります:
G =τxy / γxy =F/A / Δx/l =Fl / AΔx
- G はせん断係数または剛性係数です
- τxy または F/A はせん断応力
- γxy はせん断ひずみです
- せん断ひずみは Δx/l =tan θ または場合によっては =θ
- θ は、加えられた力による変形によって形成される角度です
- A は力が作用する領域です
- Δx は横方向の変位です
- l は最初の長さです
せん断応力の計算例
たとえば、4×10 N/m の応力下にあり、5×10 のひずみが発生しているサンプルのせん断弾性率を見つけます。
G =τ / γ =(4×10 N/m) / (5×10) =8×10 N/m または 8×10 Pa =800 KPa
等方性および異方性材料
材料は、せん断に関して等方性または異方性のいずれかです。等方性材料の変形は、加えられた力に対する方向に関係なく同じです。対照的に、異方性材料の応力または歪みは、その方向に依存します。
多くの一般的な材料は異方性です。たとえば、ダイヤモンド結晶 (立方晶) は、力が結晶格子と整列すると、はるかに容易にせん断します。四角い木のブロックは、木目に平行に力を加えるか垂直に力を加えるかによって、力に対する反応が異なります。等方性材料の例には、ガラスや金属が含まれます。
温度と圧力への依存
温度と圧力は、加えられた力に対する材料の反応に影響を与えます。通常、温度を上げるか圧力を下げると、剛性とせん断弾性率が低下します。たとえば、ほとんどの金属は加熱すると加工しやすくなりますが、冷却するともろくなります。
せん断弾性率に影響を与えるその他の要因には、融点と空孔形成エネルギーが含まれます。
Mechanical Threshold Stress (MTS) 塑性流動モデル、Nadal and LePoac (NP) せん断応力モデル、および Steinberg-Cochran, Guinan (SCG) せん断応力モデルはすべて、せん断応力に対する温度と圧力の影響を予測します。これらのモデルは、科学者やエンジニアが、せん断応力の変化が線形である温度と圧力の範囲を予測するのに役立ちます。
せん断弾性率値の表
材料のせん断弾性率の値は、その温度と圧力によって異なります。これは、代表的な物質の室温でのせん断弾性率の値の表です。低いせん断弾性率の値は柔らかく柔軟な材料を表しますが、硬くて硬い物質は高いせん断弾性率の値を表します。たとえば、遷移金属、それらの合金、およびダイヤモンドは、せん断弾性率の値が高くなります。ゴムと一部のプラスチックは低い値です。
| 素材 | せん断弾性率 (GPa) |
| ラバー | 0.0006 |
| ポリエチレン | 0.117 |
| 合板 | 0.62 |
| ナイロン | 4.1 |
| 鉛 (Pb) | 13.1 |
| マグネシウム (Mg) | 16.5 |
| カドミウム (Cd) | 19 |
| ケブラー | 19 |
| コンクリート | 21 |
| アルミニウム (Al) | 25.5 |
| グラス | 26.2 |
| 真鍮 | 40 |
| チタン (Ti) | 41.1 |
| 銅 (Cu) | 44.7 |
| 鉄 (Fe) | 52.5 |
| スチール | 79.3 |
| ダイヤモンド (C) | 478.0 |
せん断弾性率、ヤング率、体積弾性率
せん断弾性率、ヤング率、および体積弾性率は、フックの法則に従って、それぞれ材料の弾性または剛性を表します。ヤング率は、固体の変形に対する剛性または線形抵抗を測定します。体積弾性率は、材料の圧縮に対する抵抗力の尺度です。各弾性係数は、次の式を介して互いに関連しています:
2G(1+υ) =E =3K(1−2υ)
- G はせん断弾性率です
- E はヤング率
- K は体積弾性率
- υ はポアソン比です
参考文献
- スティーブン、クランダル。ラードナー、トーマス (1999)。 固体の力学入門 (第2版)。マグロウヒル。 ISBN:978-0072380415.
- Guinan, M.;スタインバーグ、D. (1974)。 「65 要素の等方性多結晶せん断弾性率の圧力と温度の微分」。 Journal of Physics and Chemistry of Solids . 35 (11):1501. doi:10.1016/S0022-3697(74)80278-7
- Landau, L.D.;ピタエフスキー、LP。 Kosevich、A.M。 Lifshitz、E.M. (1970)。 弾性の理論 (第3版)。巻。 7.オックスフォード:ペルガモン。 ISBN:978-0750626330.
- ナダル、マリー エレーヌ。ル・ポアック、フィリップ(2003)。 「融点までの圧力と温度の関数としてのせん断弾性率の連続モデル:分析と超音波検証」. Journal of Applied Physics . 93 (5):2472. doi:10.1063/1.1539913
- Varshni, Y. (1981). 「弾性定数の温度依存性」。 フィジカル レビュー B . 2 (10):3952.