行列は、行に配置された数値または方程式の表現形式です。長方形のテーブルまたはボックスのような列。行と列の数は、行列の次元を指定します。たとえば、行列が 3 行 4 列の場合、それは 3*4 行列と呼ばれます。行列の積は、行列に関連する特定の規則と線形代数に従います。行列の乗算は算術演算に基づいており、数学および研究分野で多くの用途があります。マトリックスに格納された複雑な値と関係を変換および分析するためのベースを提供します。
行列の表現
最初のステップは、適切な形式で行列を記述して、算術演算が正しく行われるようにすることです。操作を簡単に実行できます。
3 行 4 列の行列 X があるとします。
m と n は行数を表す Xmn として表されます。および列をそれぞれ指定します。したがって、Xmn =X34
行列 X にいくつかの値を入力してみましょう。X3*4 =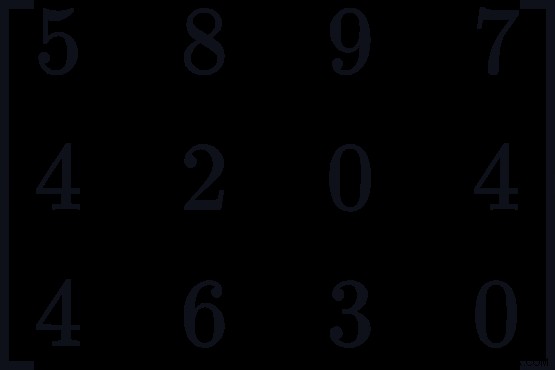
ここで、スペースは新しい列が始まったことを示し、カンマは、つまり、「,」は新しい行を表します。
たとえば、5 は最初の行と最初の列に属し、 3 は 3 行 3 列目に属します。
行列の積の性質
行列の積に関連するさまざまな基本的なプロパティがあり、以下を含みます:
Commutative Property:2 つの行列、つまり X と Y の積は可換ではありません。したがって、XY ≠ YX です。
Associative Property:3 つの行列、つまり X、Y、Z の積は結合的です。したがって、X(YZ) =(XY)Z.
分配特性:X、Y、Z の 3 つの行列の積は分配的です。したがって、X(Y + Z) =XY + YZ です。
行列の積 – 行列にスカラーを掛けたもの
スカラー量による行列の乗算は、基本的な乗算方法です。これは、行列のすべての値がスカラー値で乗算される、行列の最も単純で高速な乗算です。
行列 X3*2 =を考えてみましょう 
およびスカラー値 5.
行列 X とスカラー値 5 の積は
P =5*X3*2 =5
最終積は P =
すべての行と列の値にスカラー値が乗算されます。マトリックスの次元は変更されません。
行列の積の条件
行列の乗算は、最初の行列の列数が2 番目の行列の行数に等しい。これにより、両方の行列の各値が乗算され、新しい行列の要素が形成されます。
2 つの行列 X3*3 と Y3*2 を考えてみましょう。行列 X の列は、行列 Y の行数と同じです。つまり、両方とも値 =3 です。
行列積は P =XY で表されます。
結果のマトリックスでは、行と列の数は最初の行列の行数 (X) と 2 番目の行列の列数 (Y) です。
ここで、結果の行列 P は P3*2 で表されます。
一般に、X と Y の次元が (m,n) で、 (q,r) は、それぞれ Xm*n および Yq*r として表され、P、つまり X と Y の積によって形成される行列は、Pm*r として表されます。
この場合、結果の行列の次元が変わります。つまり、どの親行列の次元とも等しくありません。
例
2 つの行列 X2*3 =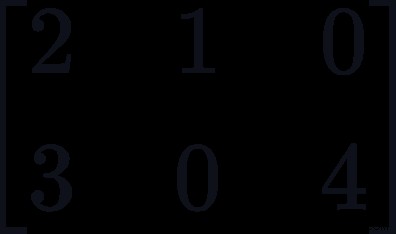
および Y3*4 =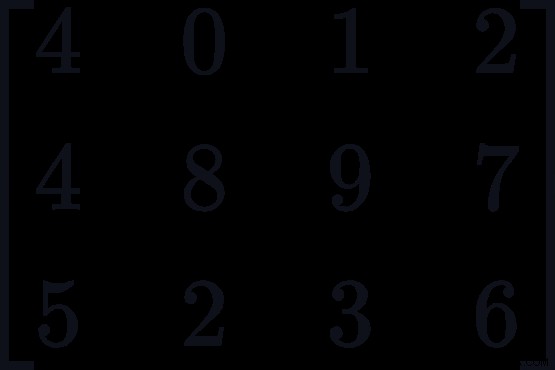
ここで、行列 X の行数は、行列 Y の列、つまり両方とも 3 に等しい
行列 X と Y を乗算します:
X*Y =*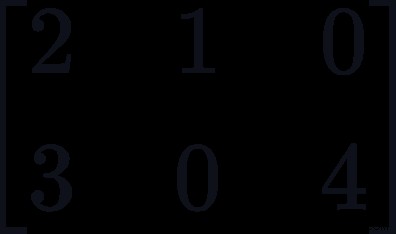
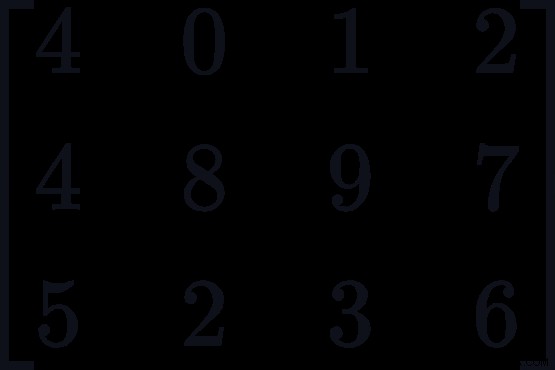
ここで、行列 X の最初の行に行列のすべての列を掛けます。 Y を一度に 1 つずつ実行し、行列 X の残りの行に対してプロセスを繰り返します。
したがって、
* 
=2*4 + 1*4 + 0*5 =12
* 
=8
* 
=11
* 
=11
同様に、行列 X の 2 行目について、
* =32
* =8
* =15
* =30
したがって、結果の行列は P2*4 =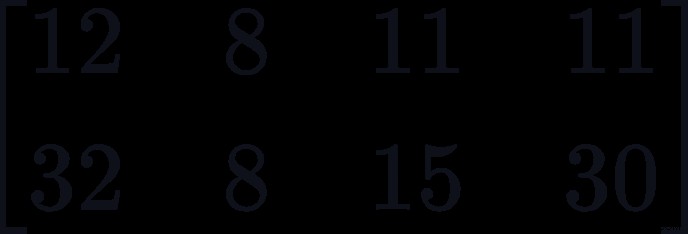
結論
行列の乗算は、画像の形成中にデータのセグメントを処理する場合に役立ちます。変換、およびその他の数学的問題。複雑な代数、三角法、複素数などの幅広い領域をカバーしています。これにより、行列乗算の主な用途は、各セグメントの詳細な調査を必要とする画像処理およびオブジェクト変換の分野です。このため、行列の乗算は、高度な数学を必要とするさまざまな複雑なセグメントに分割されます。
