摩擦係数の寸法式|物理

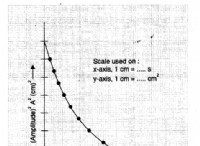
次元式:身体量の次元式は、その量でどの底部がどのように保護されているかを表す式として定義されます。適当な強度の土台部分の記号を[ ]のように角括弧で囲んで表記します。例として質量の寸法式を[M]とします。

摩擦は、運動中または運動状態になろうとする 2 つの表面間の抵抗力です。摩擦係数はギリシャ記号 (μ) で表されます

静摩擦係数

摩擦係数は、材料固有の特性です。つまり、材料の性質のみに依存します。滑らかな表面は摩擦係数が小さく、粗い表面は摩擦係数が大きくなります。分子レベルでは、材料表面の分子の不均一な配置が原因で発生します。

静止摩擦力は、垂直抗力と静止摩擦係数の積です。次のように書くことができます

Fs =μsN

ここで、

Fs -静止摩擦力の最大値

μs -静摩擦係数、

N – 法線力、

静止摩擦係数はスカラー量です。単位や次元はありません。通常、静止摩擦係数は 0 ～ 1 の範囲です。0 に近い場合、2 つのオブジェクト間に摩擦はありません。一方、1 に近い場合、オブジェクト間の摩擦は垂直抗力に等しくなります。摩擦力が法線力よりも強い場合、係数がより重要になる場合があります。

摩擦係数は、摩擦力とそれらの間に作用する法線力の比率であるため、無次元の量、つまり (μ) =f/N

f =摩擦力;

N =通常の力

摩擦力の寸法式＝MLT-2

同様に、垂直力の寸法式 =MLT-2

したがって、[μ] =MLT-2/MLT-2 =1.

上記の導出は、摩擦係数が無次元量であることを証明しています。

摩擦はエネルギーを散逸させる単なる力のように思えるかもしれませんが、コインの裏側には、さまざまな方法で私たちを助けているということもあります。摩擦の最も重要な利点は、摩擦によって紙に書くことができることです。

転がる物体の重量に対する転がり摩擦力の比率です。

μr =Fr / W …………. (N =W)

𝜇𝑠 は静摩擦係数、𝜇𝑘 は動摩擦係数、𝜇r は転がり摩擦係数です。

𝜇𝑠> 𝜇𝑘>𝜇r

摩擦係数は基本的に、2 つのオブジェクト間に作用する力とそれらを押し付ける力の比率です。これは材料の内部特性であり、体の表面の分子の不規則な配置によって発生します。これは無次元の量であり、(μ) で表されます。