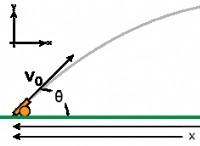
この関係は、次の方程式から見ることができます。
$$ v_f^2 =v_i^2 + 2ad $$
どこ:
- \(v_f \)は、オブジェクトの最終速度です(最大高さに達すると0 m/sです)
- \(v_i \)は、オブジェクトの初期速度です
- \(a \)は重力による加速です(-9.8 m/s^2)
- \(d \)はオブジェクトの変位です(これは到達する最大高さです)
\(d \)のこの方程式を解くと、次のようになります。
$$ d =\ frac {v_i^2} {2a} $$
この方程式は、オブジェクトによって到達する最大高さが初期速度の平方に比例していることを示しています。言い換えれば、初期速度を2倍にすると、オブジェクトは高さの4倍に達します。
この関係は、次の表に見ることができます。
|初期速度(m/s)|最大高さに達した(m)|
| --- | --- |
| 10 | 5 |
| 20 | 20 |
| 30 | 45 |
| 40 | 80 |
| 50 | 125 |
ご覧のとおり、オブジェクトによって達する最大高さは、初期速度が増加すると劇的に増加します。