数学的には、周波数は波の期間(t)の逆(t)として計算されます。これは、1つの完全な振動またはサイクルにかかる時間です。頻度と期間の関係は、次のように表現できます。
f =1 / t
周波数が異なる波の特性とどのように関連するかは次のとおりです。
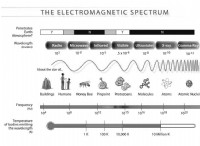
1。波長:周波数は波長(λ)に反比例します。より長い波長はより低い周波数に対応しますが、より短い波長はより高い周波数に対応します。この関係は、電磁スペクトルなどのさまざまな波の現象で見ることができます(たとえば、無線波はX線と比較して長い波長とより低い周波数を持っています)。
2。波速度:周波数と波速度(v)は直接比例します。波の速度は、波が培地を通って移動する速度です。より高い周波数の波は、より低い周波数の波よりも速く移動します。この関係は、音波や水波などの機械的波で一般的に観察されます。この波は、より高いピッチの音(高い周波数)が低い音の音よりも速く移動します。
3。時間領域表現:時間領域では、時間の経過とともに振動する関数として波を表すことができます。波の周波数は、この振動がどれだけ速く発生するかを決定します。周波数が高いと振動が速くなりますが、周波数が低いと振動が遅くなります。
4。周波数スペクトル:多くのアプリケーションでは、波または信号に存在する周波数成分を分析することが有用です。これは、Fourier分析などの手法を使用して実行できます。これにより、信号が構成要素周波数成分に分解されます。結果の周波数スペクトルは、異なる周波数にわたるエネルギーまたは振幅の分布に関する洞察を提供します。
物理学、エンジニアリング、音響、通信など、さまざまな分野で頻度を理解することは重要です。これにより、定期的な現象を定量化および分析し、楽器の調整から電子システムの情報の処理と送信まで、多様なアプリケーションで基本的な役割を果たします。