これがその起源の内訳です:
1。ブラウンモーションとランジュビン方程式:
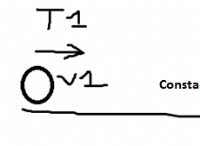
*基礎は、液体に吊り下げられた粒子の一見ランダムな動きであるブラウン運動の観察にあります。
* アルバート・アインシュタイン およびマリアンスモルチョウスキー 統計力学を使用してこの動きを説明し、周囲の液体の分子による粒子の連続砲撃によって引き起こされることを示しています。
* ポール・ランジュビン 後に微分方程式(ランゲビン方程式)を定式化して、決定論的な力(摩擦など)とランダムな力の両方に影響する粒子の動きをモデル化しました。
2。ランゲビンを確率に接続する:
* Langevin方程式は、単一の粒子の軌跡を説明しています。多くの粒子の集合的な動作を理解するには、確率分布で作業する必要があります。
* Andrey Kolmogorov adriaan fokker Langevin方程式に確率的アプローチを適用することにより、Fokker-Planck方程式を独立して開発しました。
3。派生:
*彼らは、a 拡散方程式のアイデアを使用しました 、ランダム運動による物質の拡散を説明しています。
*ランジュバン方程式のドリフトと拡散項を考慮することにより、それらは確率密度関数の時間進化を支配する部分的な微分方程式を導き出しました。
4。主な貢献:
* fokker 特定の物理モデルから方程式を導出することに焦点を当て、 planck 数学的枠組みに取り組みました。
* kolmogorov 後に方程式を一般化して、より広いクラスの確率的プロセスを記述し、コルモゴロフフォワード方程式という名前につながりました。
本質的に、Fokker-Planck方程式は、個々の粒子運動の決定論的記述(Langevin方程式)と多くの粒子の集合的な挙動の確率的記述(確率密度関数)の間のギャップを橋渡しします。
アプリケーション:
Fokker-Planck方程式は、以下を含むさまざまな分野で広範囲にわたるアプリケーションを発見しました。
* 物理学: ブラウン運動、拡散プロセス、プラズマ物理学
* 化学: 化学動態、反応拡散システム
* 生物学: 集団ダイナミクス、遺伝子発現
* 財務: オプションの価格設定モデル、資産価格設定
これは、ランダムな変動の対象となるシステムの挙動を理解し、予測するための強力なツールです。