1。中心力と重力:
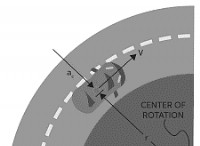
*オブジェクトが別のもの(地球の周りの衛星のように)を軌道に乗せるには、軌道の中心に向かって引っ張る力が必要です。この力は、中心力と呼ばれます 。
*軌道の場合、重力 この中心力を提供します。軌道と中央の体の間の重力引力は、それが直線で飛び出さないようにします。
2。バランス法:
*軌道がゆっくりと動いている場合、重力はそれを引き下げ、スパイラルインしてクラッシュします。
*動きすぎると、重力プルから完全に逃げて宇宙に飛び立ちます。
* 安定した軌道の場合、速度は重力プルのバランスをとるのにちょうど適切でなければなりません。
3。方程式:
軌道速度(v)、重力による加速度(g)、および軌道の半径(r)の関係は、次の方程式によって定義されます。
v²=g * r
この方程式は、を教えてくれます
* オブジェクトが速く動く(より高いV)ほど、重力(g)が特定の半径(r)で軌道に保つために必要なものである必要があります。
* 軌道が大きいほど、オブジェクトの動きが遅くなります(v)同じ重力の下で軌道にとどまる(g)。
例:
衛星を周回する地球を持っているとしましょう。その高度での地球の重力加速度(g)は9.8 m/s²です。 7,000 km(7,000,000メートル)の半径の衛星軌道の場合、その軌道速度は次のとおりです。
V²=9.8 m/s² * 7,000,000 m
V =√(9.8 m/s² * 7,000,000 m)
V≈7,668m/s
結論:
軌道速度と重力による加速度の関係は、バランスの1つです。速度は、重力プルに対抗して安定した軌道を維持するのに適している必要があります。この関係は、宇宙船、衛星、さらには惑星でさえ軌道にとどまる方法を理解するために不可欠です。