概念を理解する
* 作業: 作業は、力によってオブジェクトが特定の距離を移動させると行われます。それはエネルギー移動の尺度です。
* 力(f): 力はオブジェクトに適用されます。
* 変位: オブジェクトが移動する距離。
* 角度(θ): 力ベクトルと変位ベクトルの間の角度。
なぜコサイン?
* 有効な力: 力が角度で適用される場合、変位の方向に作用する力の成分のみが実際に行われた作業に寄与します。このコンポーネントは、有効な力と呼ばれます 。
* 救助への三角法: コサインは、直角三角形の隣接する側をhypotenuseに関連付ける三角関数です。この場合:
* hypotenuse: 力(f)
* 隣接する側: 有効な力(f *cosθ)
アクションの式
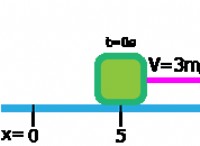
1。視覚化: 床に箱を押すと想像してみてください。力を下向きと前方に適用しますが、ボックスは水平方向にのみ移動します。力とボックスの変位の間の角度は角度θです。
2。分解: フォースを2つのコンポーネントに分割します。
* 水平成分(f *cosθ): このコンポーネントは変位に平行で、機能します。
* 垂直成分(f *sinθ): このコンポーネントは変位に垂直であり、機能しません(ボックスが垂直に動いていないため)。
3。計算: 行われた作業は、効果的な力と変位の産物です。
* w =(f *cosθ) * s
キーテイクアウト
*作業はスカラー量です(大きさはありますが、方向はありません)。
*変位の方向に作用する力の成分のみが機能します。
*コサイン関数により、力と変位の間の角度を考慮することにより、効果的な力を見つけることができます。