直接的な関係:
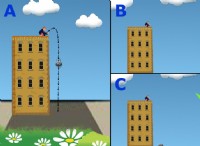
* 一定の加速: オブジェクトが一定の速度で加速すると、それが覆う距離は時間とともに増加します。加速度が速いほど、特定の時間で覆われた距離が大きくなります。この関係は、次の運動学的方程式によって説明されています。
* d =v₀t +½at²
* d =距離
*v₀=初期速度
* t =時間
* a =加速
* コンセントのない加速: 加速度が一定でない場合、加速度と距離の関係がより複雑になります。距離を正確に計算するために、加速が時間とともにどのように変化するかを考慮する必要があります。
例:
* 車の加速: 車が安静から加速すると、長時間加速するにつれて距離が長くなります。車が加速するほど速くなるほど、同じ時間で移動します。
* 落下オブジェクト: 重力の下で自由に落ちるオブジェクトは、一定の速度(9.8 m/s²)で加速します。それが落ちるにつれて、それが覆う距離は、一定の加速により時間とともに急速に増加します。
キーポイント:
* 初期速度: オブジェクトの初期速度も、覆われた距離に影響します。初期速度が高いオブジェクトは、同じ加速度であっても、休息から始まる距離よりも多くの距離をカバーします。
* 時間: オブジェクトが加速するのが長いほど、カバーする距離が大きくなります。
* 方向: 加速度は正または負になります(減速または減速)。負の加速度は、加速なしまたは陽性加速度と比較して、覆われた距離を減らします。
要約: 加速度は、オブジェクトが移動する距離に直接影響します。加速度が大きいほど、特定の時間にわたって距離が大きくなります。この関係は、加速度が一定ではない場合に複雑であり、加速が時間とともにどのように変化するかをより詳細に分析する必要があります。