1。質量:
* 直接比例: 中心力は、円内で移動するオブジェクトの質量に直接比例します。これはつまり:
* より多くの質量=より多くの力: より重いオブジェクトは、同じ円運動を維持するために、より大きな中心力を必要とします。
* 質量が少ない=力が少ない: 軽いオブジェクトには、より小さな中心力が必要です。
2。半径:
* 逆比例: 中心力は、円形経路の半径に反比例します。これはつまり:
* より大きな半径=より小さな力: より大きな半径の場合、オブジェクトは、円形の経路にとどまるために、より少ない求心力が必要です。
* 半径が小さい=より大きな力: 半径が小さい場合、オブジェクトは円形の経路にとどまるためにより多くの中心力を必要とします。
式と説明
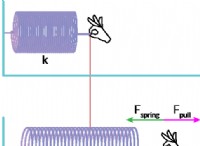
Centripetal Force(FC)の式は、これらの関係をカプセル化します。
fc =(m *v²) / r
どこ:
* fc: 求心力
* m: オブジェクトの質量
* V: オブジェクトの速度
* r: 円形経路の半径
キーポイント
* 速度: 式は速度の四角を示していますが、中心力と速度の関係は複雑です。より高い速度では、オブジェクトを円に動かし続けるには大きな力が必要ですが、関係は単に比例するわけではありません。
* その他の要因: 中心力は、オブジェクトの速度や、中心力(例えば、重力、弦の張力、摩擦)を提供する力のタイプなどの他の要因の影響を受けます。
例
* 角を曲がる車: より重い車は、より軽い車よりも角を曲がるためにタイヤからより多くの力を必要とします。
* 軌道の衛星: 地球からさらに周回する衛星は、地球の近くに周回する衛星よりも軌道にとどまるために少ない重力力を必要とします。
特定の例を探索したり、これらの概念の背後にある数学を深く掘り下げたい場合はお知らせください!