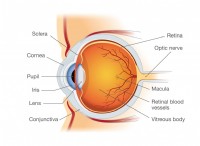
f =(mv^2)/r
どこ:
* f 中心部の力です(ニュートンで測定)
* m オブジェクトの質量です(キログラムで測定)
* v オブジェクトの速度です(1秒あたりのメートルで測定)
* r 円形経路の半径(メートルで測定)です
この方程式に関与する乗算はありません。 方程式自体は、中心力、質量、速度、および半径の関係を表す単一の式です。
ただし、遠心力の実際の値を計算するには、乗算を実行する必要があります。
*質量(m)に速度の正方形(v^2)を掛けます。
*その後、その製品を半径(R)で除算します。
例:
5 m/sの速度で半径1メートルの円で2 kgの質量を移動するオブジェクトがあるとしましょう。
* m =2 kg
* v =5 m/s
* r =1 m
計算:
* f =(mv^2)/r
* f =(2 kg *(5 m/s)^2)/1 m
* f =(2 kg * 25 m^2/s^2)/1 m
* f =50 n
したがって、オブジェクトに作用する中心力は50のニュートンです。