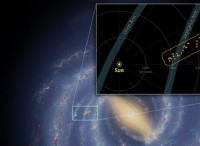
w =f * d * cos(θ)
どこ:
* w 作業は行われています
* f 力の大きさです
* d 変位の大きさです
* θ 力ベクトルと変位ベクトルの間の角度です
説明:
* 変位方向の力成分: 力ベクトルは、変位(f * cos(θ))に平行な2つの成分と、変位(f * sin(θ))に垂直な1つの成分に分解できます。変位に平行な力の成分のみが機能します。
* 並列コンポーネントによって行われた作業: 力の平行成分によって行われる作業は、コンポーネントの大きさに変位を掛けたものに等しくなります。
* コセイン関数: コサイン関数は、変位に平行な力の成分を見つけるために使用されます。
キーポイント:
*角度θは、力ベクトルと変位ベクトルの間の角度であり、力ベクトルと水平または垂直軸の間の角ではありません。
*行われた作業はスカラー量です。つまり、大きさはありますが、方向はありません。
*行われた作業は、力と変位が同じ方向にあり、反対方向にある場合は否定的な作業です。
例:
10 nの力が、変位方向まで30度の角度でオブジェクトに適用されます。オブジェクトは5メートル移動します。完了した作業を計算します。
* f =10 n
* D =5 m
*θ=30度
w =10 n * 5 m * cos(30°)=43.3 j
したがって、オブジェクトで行われた作業は43.3ジュールです。