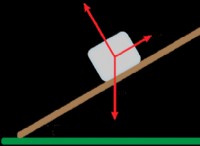
滑りやすいスライド
問題:
体重が30 kgの子供は、30度の傾斜で5メートルの長さのスライドの上部にあります。子とスライドの間の運動摩擦係数は0.2です。子供が休息から始まる場合、スライドの底での速度はどれくらいですか?
解決策:
1。力を識別します:
* 重力(重量): M =30 kg(質量)およびg =9.8 m/s²(重力による加速)の大きさで、垂直方向に下向きに作用します。
* 通常の力: スライドに垂直な作動は、スライドに垂直な重力の成分を打ち消します。
* 摩擦: スライドに平行な動作は、μnの大きさで動きに対立し、μ=0.2(運動摩擦係数)とnが正常な力です。
2。力:
* スライドに平行: スライドに平行な重力の成分はmg sin(30°)であり、子供を追い払う。
* スライドに垂直: スライドに垂直な重力の成分はmg cos(30°)であり、通常の力(n =mg cos(30°))のバランスが取れています。
3。ニュートンの第二法則を適用します:
* 正味力=質量×加速
*子供に作用する正味の力はmg sin(30°)-μn=maです。
4。加速度を解決:
* N =mg cos(30°)を方程式に置き換えます。
* mg sin(30°)-μ(mg cos(30°))=ma
* a =g(sin(30°)-μcos(30°))
* a =9.8 m/s²(0.5-0.2×0.866)≈3.15m/s²
5。運動学を使用して速度:を見つけます
*初期速度(v₀=0 m/s)、加速(a≈3.15m/s²)、および距離(d =5 m)を知っています。
*運動学的方程式を使用:v²=v₀² + 2ad
*v²=0² + 2×3.15 m/s²×5 m
*v²≈31.5
*V≈√31.5≈5.61m/s
したがって、スライドの下部にある子供の速度は約5.61 m/sです。