キーポイント:
* 仮定: 分布は、次の仮定に基づいて導出されます。
*ガスは理想的です。つまり、粒子は弾性衝突を除いて相互作用しないことを意味します。
*粒子は熱平衡状態にあります。つまり、一定の平均運動エネルギーを持っています。
*粒子はすべての方向にランダムに動いています。
* 分布: Maxwell分布は、ガスからランダムに選択された粒子が特定の速度 *V *を持つ可能性を与えます。確率密度関数は次のように与えられます。
`` `
f(v)=4π(m /(2πkt))^3/2 * v^2 * exp(-mv^2 / 2kt)
`` `
どこ:
* * f(v) *は、速度で粒子を見つける確率密度 * v *
* * m *は単一の粒子の質量です
* * k *はボルツマン定数です
* * t *は絶対温度です
* 解釈:
*分布は、最も可能性の高い速度でピークがあるベル型の曲線です。
*平均速度は、最も可能性の高い速度よりもわずかに高くなります。
*より高い温度では分布が広く、粒子の速度が広いことを示しています。
重要性:
* ガス行動の理解: Maxwell分布は、圧力、粘度、熱伝導率など、ガスの多くの観察された特性を説明しています。
* アプリケーション: 分布には、以下を含む多くの分野にアプリケーションがあります。
* 化学動態: 反応速度の予測
* 血漿物理学: 荷電粒子の挙動を説明します
* 天体物理学: 星と星間ガスのダイナミクスを理解する
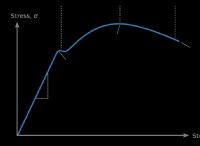
視覚表現:
Maxwell分布は、多くの場合、X軸上の速度(V)とY軸の確率密度(F(v))を含むグラフとして描かれています。曲線はそれを示しています:
*ほとんどの粒子には、最も可能性の高い速度に近い速度があります。
*粒子が少ないか、非常に低いか非常に高速です。
*曲線の形状は温度とともに変化します。温度が高くなると、速度がより広く分布します。
要約:
速度のマックスウェル分布は、ガスの挙動を理解するための基本的なツールです。それは、熱平衡状態でのガス中の粒子の速度の分布に関する確率論的な説明を提供し、観察された特性を説明し、さまざまな科学分野の進歩に寄与します。