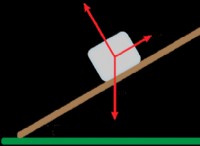
* より高い慣性モーメント: たわみが少ないにつながります
* 慣性の低いモーメント: より多くの偏向につながります
ここに理由があります:
慣性モーメント 曲げに対するビームの抵抗の尺度です。それは本質的に、梁の断面形状が曲げ力に抵抗するためにその材料をどのように分布させるかを説明しています。
drection 梁が荷重下で曲がる量です。
このように考えてください:
* 慣性モーメントが大きい(広くて深いIビームのような)ビームは、強くて頑丈な板のようなものです。 それはあまり偏向することなく、より多くの曲げ力に耐えることができます。
* 慣性モーメントが小さく(薄く狭いビームのような)beamは薄っぺらな小枝のようなものです。 わずかな負荷でも大幅に曲がります。
ビーム偏向の方程式は、この関係を強調しています:
`` `
たわみ(δ)=(p * l^3) /(3 * e * i)
`` `
どこ:
* p 適用された負荷です
* l ビームの長さです
* e 材料の弾性率です
* i 慣性の瞬間です
この方程式は、たわみがiに反比例するであることを示しています 。
実際的な意味:
* より強いビーム: たわみを最小限に抑え、より安定した構造を作成するには、より大きな慣性モーメントを持つビームを使用します。これは、次のことを達成できます。
*ビームの断面領域を増やします
*ニュートラル軸からさらに分布した材料で形状を選択する(iビームのように)
* 軽量構造: 軽量構造を設計するとき、エンジニアは、材料の使用量を減らすために、慣性の瞬間が低い形状を選択する場合があります。これはより大きな偏向につながる可能性がありますが、設計の制約に応じて受け入れられる可能性があります。
結論、 慣性の瞬間は、荷重の下でどれだけビームが偏向するかを決定する上で重要な役割を果たします。この関係を理解することにより、エンジニアは適切なビームの形状とサイズを選択して、その構造の望ましい剛性と強度を実現できます。