速度との関係:
* 直接比例: 中心性加速(AC)は、オブジェクトの速度(v)の正方形に *直接比例 *です。これは、速度を2倍にすると、中心加速度の象限を2倍にすることを意味します。
* 方程式: ac =v²/r
半径との関係:
* 逆比例: 中心性加速度は、円形経路の半径(r)に *逆比例 *です。これは、半径を2倍にすると、中心形状の加速度が半分になることを意味します。
* 方程式: ac =v²/r
要約:
* より高い速度、より高い加速: 円を移動するより速いオブジェクトには、円形経路を維持するために、より大きな中心性加速が必要です。
* より大きな半径、低い加速: より大きな円を移動するオブジェクトは、より少ない求心性加速度を必要とします。
例:
車が円形のトラックを回っていると想像してみてください。
* 速度の増加: 車のスピードが上がると、トラックにとどまるにはより多くの求心性加速が必要です。これが、車が角を曲がって速すぎる場合、車が滑る可能性がある理由です。
* より広いターン: トラックの曲線が広い場合(半径が大きい)、車の継続的な加速度が少ないため、トラックにとどまる必要があります。これが、車が高速でより広い曲線を安全に取ることができる理由です。
重要な概念:
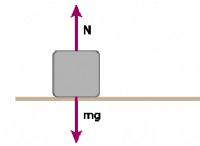
速度、半径、および中心の加速の関係は、円運動の物理学を理解するために不可欠です。それは、なぜ円の動きのオブジェクトが一定の内向きの力を経験するのか、そして彼らの経路を維持するために特定の量の加速を必要とする理由を説明します。