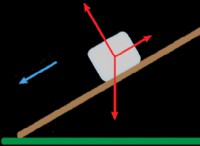
力を理解する
* 中心力: これは、オブジェクトを円で動かし続ける力です。常に円の中心に向けられています。この場合、摩擦力によって中心力が提供されます。
* 摩擦力: この力はオブジェクトの動きに反対し、接触表面と平行に作用します。この場合、円の中心に向かって作用します。
重要な方程式
* 中心力: f_c =(mv^2)/r where:
* f_cは中心力です
* mはオブジェクトの質量です
* vはオブジェクトの速度です
* rは円形経路の半径です
* 摩擦力: f_f =μnwhere:
* f_fは摩擦の力です
*μは摩擦係数です
* nは正常な力です(この場合はmgに等しく、Gは重力による加速です)
最大速度を導出します
1。等しい力: 摩擦の力は求心力を提供しているため、互いに等しい方程式を設定できます。
μn=(mv^2)/r
2。通常の力の置換: 代用n =mg:
μmg=(mv^2)/r
3。速度の解決: 質量(m)をキャンセルし、方程式を再配置して速度(v)を解くようにします。
V^2 =μgr
v =√(μgr)
したがって、摩擦係数(μ)を持つ半径(r)の円形経路でオブジェクトが維持できる最大速度(v)は、式で与えられます:v =√(μgr)
重要なメモ:
*この方程式は最大速度を与えます。オブジェクトの速度がこの値を超えると、摩擦の力はそれを円形の経路に保つのに十分ではなく、外側にスライドします。
*この導出は、静的摩擦係数を想定しています。オブジェクトがすでに動いている場合、速度摩擦係数がより適切になる可能性があります。
*この分析では、平らな表面を想定しています。表面が傾斜している場合、通常の力と最大速度が変化します。