1。変位、速度、および加速
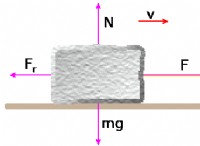
* 変位(x): 粒子の位置の最初の位置からの変化。
* 速度(v): 時間に対する変位の変化率。ベクトル量(大きさと方向)です。
* 加速(a): 時間に対する速度の変化率。ベクトル量でもあります。
2。運動方程式(一定加速度)
一定の加速度の動きには、次の方程式があります。
* 速度時間方程式: v =u + at
* v =最終速度
* u =初期速度
* a =加速
* t =時間
* 変位時間方程式: x =ut +(1/2)at^2
* x =変位
* u =初期速度
* a =加速
* t =時間
* 速度分解方程式: v^2 =u^2 + 2Ax
* v =最終速度
* u =初期速度
* a =加速
* x =変位
3。その他の重要な概念
* 発射体の動き: 重力の影響下で空気中に発射されたオブジェクトの動き。
* 円形運動: 中心部の加速度を特徴とする円形経路での動き(円の中心に向けられています)。
* 単純な高調波運動(SHM): 回復力が平衡からの変位に比例する特別なタイプの振動運動。
4。運動方程式の例
* 線形運動: x(t)=x0 + v0t +(1/2)at^2(x0は初期位置、v0は初期速度です)
* 発射体の動き:
* x(t)=x0 + v0x t
* y(t)=y0 + v0y t-(1/2)gt^2(ここで、gは重力による加速度です)
* 円形運動:
* x(t)=r cos(ωt)
* y(t)=r sin(ωt)(ここで、rは半径、ωは角速度です)
5。運動方程式を導出する方法
* 計算: 速度(v =dx/dt)と加速度(a =dv/dt)の定義を使用して、積分を通じて運動方程式を導出できます。
* ベクトル代数: ベクトルを使用して変位、速度、および加速度を表すと、大きさと方向の両方を説明する方程式を取得できます。
特定のタイプの動きの詳細な説明が必要な場合、またはこれらの方程式を適用する方法の例を見たい場合はお知らせください。