基本を理解する
* 射影: 重力のみの影響を受ける空気中を移動するオブジェクト。
* 初期速度: オブジェクトが上向きにスローされる速度。
* 起動角: オブジェクトがスローされる角度(0°は水平で、90°はまっすぐになります)。
* 重力: 重力による一定の加速(約9.8 m/s²、常に下向きに動作します)。
重要な方程式
* 垂直変位:
* `Δy=v₀y * t +(1/2) * g *t²`
* どこ:
*「Δy`は垂直変位です(高さの変化)
* `v₀y`は初期垂直速度です
* `t`は時間です
* `g`は重力による加速です
* 水平変位:
* `Δx=v₀x * t`
* どこ:
* `Δx`は水平変位です(水平に移動した距離)
* `v₀x`は初期の水平速度(定数)です
* 最終速度:
* `v =v₀ + g * t`
* どこ:
* `v`は最終速度です
* `v₀`は初期速度です
* `g`は重力による加速です
* `t`は時間です
「スローアップ」の問題を解決します
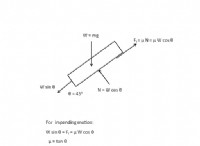
1。図を描く: 状況をスケッチし、初期速度、起動角、およびオブジェクトが最高点に達するポイントにラベル付けされます。
2。初期速度を分解:
*水平コンポーネントを見つけます( `v₀x=v₀ * cos(θ)`)
*垂直コンポーネントを見つけます( `v₀y=v₀ * sin(θ)`)
3。見つけなければならないものを特定します: 最大高さ、最高点に到達する時間、空気中の合計時間、範囲(水平距離)などが必要ですか?
4。適切な方程式を選択します:
*垂直変位には、上記の最初の方程式を使用します。
*水平変位には、2番目の方程式を使用します。
*最終速度(任意の時点で)の場合、3番目の方程式を使用します。
5。未知の変数を解決します。 覚えて:
*最高点では、垂直速度( `v`)は0 m/sです。
*上昇するのにかかる時間は、後退するのにかかる時間と同じです。
6。兆候について考えてみてください:
*上向きの動きは肯定的であると見なされるため、 `v₀y`は肯定的です。
*下向きの動きは負と見なされるため、「G」は負です。
例の問題
ボールは、20 m/sの初期速度でまっすぐに投げられます。
* ボールが到達する最大高さを見つけます。
* ボールが空中にある合計時間を見つける
解決策
1。図: 初期速度を示す矢印を上に向ける単純な垂直線を描画できます。
2。コンポーネント: 初期の垂直速度は20 m/sで、水平成分は0 m/sです(まっすぐに投げられるため)。
3。最大高さを見つけます:
*最大高さでは、最終的な垂直速度は0 m/sです。
*方程式を使用します: `v²=v₀² + 2 * g *Δy`
*プラグイン値: `0²=20² + 2 *(-9.8) *Δy`
*「Δy`: `Δy=20.41 m`を解きます
4。合計時間を見つけます:
*上昇する時間=落ちる時間。
*方程式を使用します: `v =v₀ + g * t`
*値のプラグイン値: `0 =20 +(-9.8) * t`
*「t」: `t =2.04 S`を解きます
*合計時間=2 * 2.04 S =4.08秒
重要なメモ
*空気抵抗は、導入物理学の問題ではしばしば無視されますが、発射体の実際の経路に影響を与える可能性があります。
*これらの方程式は一定の重力を想定しています。これは、地球の表面近くのオブジェクトの適切な近似です。
別の例の問題に取り組みたい場合はお知らせください!