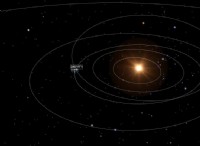
ケプラーの第二法則: 惑星を太陽に結合する線は、等しい時間間隔で等しい領域を一掃します。
これがどのように機能するかです:
* 角運動量の保存: 惑星の軌道運動は、角運動量を節約します。これは、その慣性モーメント(その質量と太陽からの距離に依存する)と角速度(回転速度)の産物の積を意味します。
* 太陽に近い、より速い軌道: 惑星が太陽に近づくと、慣性の瞬間が減少します(太陽からの距離が小さい)。一定の角運動量を維持するには、その角速度(軌道速度)が増加する必要があります。
* 太陽からさらに、より遅い軌道: 逆に、惑星が太陽から遠くにあると、慣性の瞬間が増加します。一定の角運動量を維持するには、その角速度(軌道速度)を減らす必要があります。
簡単に言えば:
太陽の周りに円形の軌道で動く惑星を想像してみてください。 惑星が太陽に近づくにつれて、同じ領域を一掃するために同じ時間で覆うスペースが少なくなります。したがって、より速く移動する必要があります。 反対は、それが太陽から遠く離れているときに起こります。
視覚アナロジー:
フィギュアスケーターが回転することを考えてください。彼らが体の近くで腕を引っ張ると、彼らはより速く回転します。彼らが腕を伸ばすと、彼らはゆっくりと回転します。 同じ原理が、太陽の周りの軌道の惑星にも当てはまります。